力扣每日一题（力扣官网）

今天开始记录力扣上刷的题目，目的就是防止偷懒。。。做题顺序的话是看那道题目不顺眼，就先把那道题目做了！若无特殊声明，所有代码语言都是python3。下面直接开始做题。

1.数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且有效的括号组合

看到这道题第一反应就是暴力法，直接列出所有可能性，然后判断是否正确就行了。但是觉得这样不是很好就没有去实现，实际操作应该是可行的。除了暴力法，还能想到什么办法呢，答案就是二叉树。因为括号分左右，而二叉树正好有左子树和右子树，所以这题其实就是搜索二叉树符合条件的节点。然后分析一下这可二叉树有什么特点：

二叉树的根节点一定是 “(“，因为如果是右括号就没有正确答案了
在左括号有剩余的情况下，就可以生成左节点，最多添加n个
插入右括号的前提是左括号的个数大于右括号（这里说的是生成节点上的，而不是剩余的括号个数）

可以画个草图看一下：

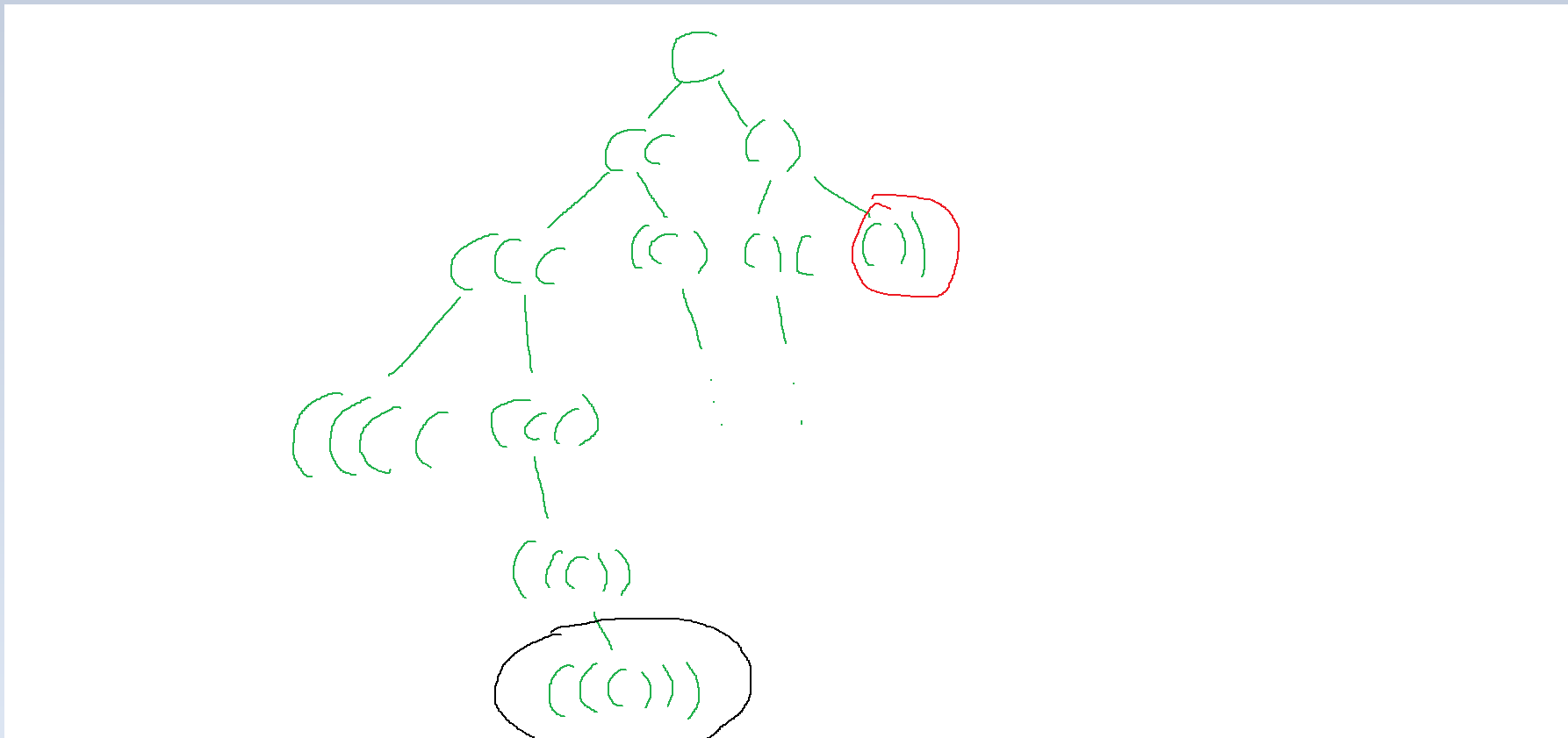
红括号中就是显然错误的分支，没有必要继续往下遍历，也就是插入右括号时没有满足第三个特点。

而黑色括号括起来的就是正确的结点。图中没有画出所有的结点。有兴趣的可以自己画画。

接下来就直接来实现代码：

首先。需要左括号，右括号的个数，然后一个result保存最终结果，tmp保存路径，也就是到达哪个节点。接下来然后直接深度遍历：

class Solution(object):
    def generateParenthesis(self, n):
        res = []
        self.dfs(res, n, n, '')
        return res
        
    def dfs(self, res, left, right, tmp):
        if left == 0 and right == 0:
            res.append(tmp)
            return
        if left > 0:
            self.dfs(res, left - 1, right, tmp + '(')
        if left < right:
            self.dfs(res, left, right - 1, tmp + ')')

2.给定一个字符串，逐个翻转字符串中的每个单词。

这道题目怎么讲呢，如果调用api的话就很简单，利用split和reverse函数，可以直接得到结果

1 2	def reverseWords(self, s: str) -> str: return " ".join(reversed(s.split()))

如果不用reversed，split，join这几个函数，要怎么实现呢？其实我一贯秉承能偷懒就绝不多动一下的理念，哈哈，所以就直接用最笨的方法吧。首先对于一个字符串，我们要将他分割为一个一个的单词，最后反向输出得到最终结果。大致思路就是这样，然后我们需要考虑一下异常情况，就是字符串首部出现空格，中间出现多个空格的情况做处理，也就是下面几种情况：

首先处理首部的字符串，确保第一个字符不为空格，如果为空格，则去除
用两个指针，来循环字符串，因为我们需要判断什么时候将字符组成一个字符串，而字符串中间出现的空格符就是标志
两个指针的另一个目的在于，当两个单词之间，出现多个空格时，单指针无法判断，我们需要双指针来判断：
- 当左指针不为空，右指针不为空，说明这个单词还没结束
- 当左指针不为空，右指针为空时，确定前面的字符组成一个单词
- 当左指针为空，右指针为空时，说明处在中间的空白符，继续向下遍历
- 当左指针为空，右指针不为空时，说明开始处理下一个单词
最后得到一个数组，里面按顺序放好单词，只要反向遍历数组，就能得到结果

直接上代码：

def reverseWords1(s):
	while True:
		# 去除头空格
		if len(s) == 0:
			return ""
		if s[0] == ' ':
			s = s[1:]
			continue
		else:
			break
	p,q = 0,1
	length = len(s)
	word  = ''
	words = []
	while True:
		##当指针到达字符串末尾时，结束循环，并将最后一个单词加入，如果是空白字符串，就不加入
		if q == length - 1:
			if s[p] != ' ' :
				word = word + s[p]
			if s[q] != ' ':
				word = word + s[q]
			if word == '' or word == ' ':
				break

			words.append(word)
			break

		if q > length - 1:
			if s[p] != ' ':
				word = word + s[p]
			if word == "" or word == ' ':
				break
			words.append(word)
			break

		if s[p] != ' ' and s[q] != ' ':
			word = word + s[p]
			word = word + s[q]
			p = p + 2
			q = q + 2

			
		elif s[p] != ' ' and s[q] == ' ':
			word = word + s[p]
			words.append(word)
			word = ''
			p = p + 2
			q = q + 2
			
		elif s[p] == ' ' and s[q] != ' ':

			words.append(word)
			word = ''
			p = p + 1
			q = q + 1
			
		elif s[p] == ' ' and s[q] == ' ':

			p = p + 2
			q = q + 2

	length = len(words) - 1
	s = ''
	while length > -1:
		if words[length] == '':
			length = length - 1
			continue
		s = s + words[length] + ' '
		length = length - 1

	length = len(s)
	s = s[:length-1]
	return s

这个代码写的很粗糙，因为只是简单实现这种思路，仅供借鉴，当不得真~

3.鸡蛋掉落

这道题目是这样的，假设你有N个蛋，这个蛋从某层楼扔下来不会碎，一旦超过这一层，就会碎，而楼共有K层，问最少扔多少次，可以找出这个临界层？

先分下一下，这里所说的最少扔多少次的意思，其实就是在最坏情况下，要扔多少次。考虑清楚这个，我们来分析一下题目。其实刚看到这个题目，第一反应就是二分法这样每次可以缩减一半的范围。然后我们现在来从最简答的情况开始分析：

N=1,K=100。也就是在这人只有一个蛋，楼层100层的情况。这种情况下显然最少要扔100次，才能确定，因为只有一个蛋，所以只能从1层开始扔，如果第一层就碎了，说明临界层为1，若是第二层碎，说明临界层为2……直到100层，所以最少次数需要100次，才能找出
N= $\infty$ ,K=100。这种情况下就可以用刚才说到的二分法，我们可以直接在50层扔，如果碎了，说明临界层在0-50，如果没有碎，说明在50-100层。然后在取中间数，直到不可以再分。显然这种情况下，可以得到一个公式 $2^{M}\ge100$ ,也就是 $M\ge \log_2100$ ,取个整数，也就是M=7

下面看稍微复杂的一些情况：

N=2，K=100。现在你有两个蛋，该如何确定临界层呢？虽然二分法不能用了，但是我们可以借鉴思路。一共有两个蛋，那么我们用第一个蛋来确定范围，我们将100 划分为0-10,10-20……这样的间隔。我们用第一个蛋在第10层，20层……100层的地方按顺序扔，如果他在某一层碎了，那么就可以用第二个蛋在刚刚的区间中来具体确定。比如说在第十层楼扔的时候碎了，那么再用第二个蛋从第一层一直扔到第九层，那么一共就需要十次。假设在第100层的时候才碎，那么从第91扔到99，又扔了9次，加上第一个蛋用来确定范围扔了十次，那么一共就是19次。这样就得到找出临界层的最少次数。我们来思考一下，虽然得到了最少次数，但是这个值是分布在10~19之间的，有没有办法让这个值更均匀一点？
首先看到造成这个值的范围的原因是因为在分间隔的时候，是等间距分的，这就造成了当第一个鸡蛋扔的范围越大时，由于第二个鸡蛋要具体确定的楼层扔的次数都为9，所以值就是这样一个范围。那么现在我们将这个间隔不均匀分布，来看看是什么情况。
依旧是 N=2，K=100。这次这样来分，第一个区域为n，第二个区域为n-1，直到最有一个区域为1，这样的话，第一个鸡蛋每确定一个区域，第二个鸡蛋所需要检验的次数也会减1。这样总次数应该会平均一些。我们来计算一下。首先确定n的值，也就是
$1 + 2 +3 +...+n = \frac{n(n+1)}{2} \ge 100$
这样n取整数为14，这样我们将100就划分为 14, 27，39，50，60, 69，77， 84， 90， 95， 99， 100。因为是取整数，所以最后不是继续加3，而是加1。那么一共分为12个区域，也就是说第一个鸡蛋最多扔十二次。如果第一个鸡蛋在14层碎了，那么需要用第二个鸡蛋来检验第1-13层，加上第一个鸡蛋扔的一次，就是14次，如果在27层碎了，那就要检验15-26层一共12层，加上第一个鸡蛋扔的两次一共14次。。。如果说第一个鸡蛋一直扔到最后一块区域才碎，那么第二个鸡蛋就不需要检验了，因为最后一个区域就一层楼，所以需要12次。也就是说按这种方式，至少需要扔14次就可以找出临界层。的确次数要比刚才的少。

其实说到现在，我们只是解决了有两个蛋的情况，下面来看看更加复杂的情况，也就是楼层和鸡蛋都不确定的情况

假设楼层为K层，鸡蛋有N个，找出临界层所需要的最少次数为M。其实要找出来的就是M关于K，N的函数，假定这个函数为M（K,N）。我们可以先整个表格看一下(列为楼层，行为鸡蛋个数)。

K\N	1	2	3
1	1	1	1
2	2
3	3

可以看到，当楼层为1或者鸡蛋个数为时，表格非常好填。但是当其都大于1时，就需要思考一下了。

需要考虑的是，第一个鸡蛋扔在哪里，其实我们也不清楚，假设第一个鸡蛋扔在了第h层，那么就得到了两种结果，一种是碎了，一种是没碎。如果碎了，说明临界层在0-H层，如果没有碎，说明在H-K层之间。那么第一种情况下，还需要扔多少次呢，这个时候其实还是相同的问题，只是楼层和鸡蛋个数的变化，即次数为M(H-1,N-1)，如果是第二种情况，那么就是M(K-H,N)。其实到这里也都看出来是个递归问题。那么因为我们需要的是最坏的情况下的次数，所以取两种情况的最大值，加上第一次扔，所以有，在你第一层鸡蛋扔在第H层情况下所需要的总次数 $M_H$ ，它就等于

$M_H = max\{M(H-1,N-1), M(K-H,N)\} + 1$

那么如何确定H呢，显然就是枚举，H取值范围1~K，即我们有 $M_1,M_2,....M_k$ ，我们的需要的是这个里面的最小值，所以就是说总次数M，就等于

$M = min\{M_1,M_2,M_3...M_K \}$

这样的话，终于算出了最终结果，其实还是挺复杂的一个问题，接下来我们就直接用代码实现吧

def throwEgg(K,N):
	#若楼高K为1，则一次
	if K == 1:
		return 1
	#创建 K+1 行 N+1列的数组(注意这里生成数组 不能使用[[0] * (N + 1)]*(K + 1)
	#因为这样生成的数组，只是生成了k+1个引用，当修改值时会一起修改从而导致bug
	res = [[0] * (N + 1) for _ in range(K + 1)]
	#如果 只有一个鸡蛋，那么次数就为楼高
	for i in range(1,N+1):
		res[1][i] = 1
	m = -1
	#遍历所有楼层的情况
	for i in range(2,K+1):
		#在指定楼层，遍历所有鸡蛋的情况，这里是通过最基本的情况，去求解复杂的情况
		for j in range(1, N + 1):
			res[i][j] = 1 + res[i - 1][j - 1] + res[i - 1][j]
		if res[i][N] >= K:
			m = i
			break
	return m

这道题目写起来挺麻烦，并且这里没有使用递归求解，感觉递归会更麻烦。这道题其实还有更多的解法，这里不展示了，有空在继续更新。

4.交点

题目描述：给定两条线段（表示为起点start = {X1, Y1}和终点end = {X2, Y2}），如果它们有交点，请计算其交点，没有交点则返回空值。要求浮点型误差不超过10^-6。若有多个交点（线段重叠）则返回 X 值最小的点，X 坐标相同则返回 Y 值最小的点。

乍一看我还觉得这道题目挺简单的。后来发现题目要求是线段而不是直线。。。然后发现这道题巨烦，倒不是多难，而是要讨论的情况太多。下面来具体看看有那些情况：

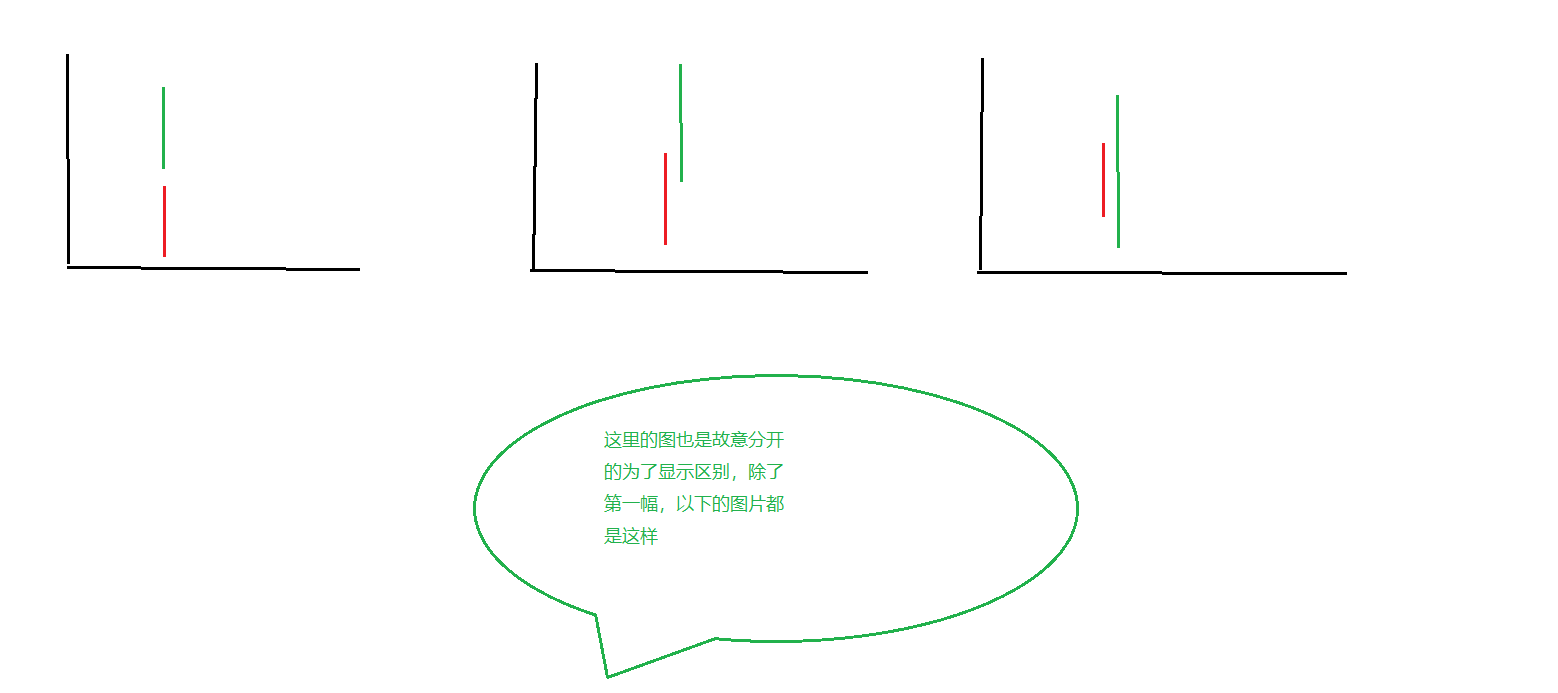
当两条线段为铅垂线时，先讨论两条直线的横坐标，若不同，则没交点，如果相同，在讨论两条线段的位置关系：先判断线段哪条的最高点更高，然后在具体讨论位置关系：
- 两条铅垂线平行，即无交点
- 两条铅垂线在一条直线上，首先要判断是否重合。这样先取两条线段中的左右端点。然后判断两条线段在纵轴上谁更”高”一点。在比较以后，将较高的那条线段叫第一条线FL,较低的那个端点为（fminx，fminy）,较高的那点记做（fmaxx，fmaxy）剩余的那条叫SL，较低的那个端点为（sminx，sminy）,较高的那点记做（smaxx，smaxy）。然后在分情况讨论：
  - 当fminy > smax的时候，两线段无交点。
  - 当fminy <= smax的时候，线段相交，然后需要讨论fminy与sminy的关系：
    1. fminy < = sminy,说明FL包含了SL，那么按题目要求交点即为(sminx,sminy)
    2. fminy > sminy,说明FL与SL相交，那么按题目要求交点即为(sminx,fminy)
当两条线段为水平线时，先讨论两条直线的纵坐标，若不同，则没交点，如果相同，在讨论两条线段的位置关系：先判断线段哪条在坐标轴上更靠右，将较右的那条线段叫第一条线FL,较左边的那个端点为（fminx，fminy）,较右边的那点记做（fmaxx，fmaxy）剩余的那条叫SL，较左的那个端点为（sminx，sminy）,较右的那点记做（smaxx，smaxy）然后在具体讨论位置关系：
- 两条水平线平行，即无交点
- 两条水平线在一直线上，然后继续分情况讨论：
  - 当fminx > smaxx，无交点
  - 当fminx <= smaxx,线段相交，然后讨论fminx与sminx的关系：
    1. fminx <= sminx,说明FL包含了SL，那么按题目要求交点即为(sminx,sminy)
    2. fminx > sminx, 说明FL与SL相交，那么按题目要求交点即为(fminx,fminy)
当斜率相同即平行时，若截距不同，则无交点，若截距相同，则在具体讨论位置关系，依旧将线段分为FL,SL，端点依旧是大的设为max，小的叫min
- 当fminx > smax 的时候，无交点
- fminx <= smax 时：
  - fminx <= sminx，交点就为(sminx,sminy)
  - fminx > sminx, 交点就为(fminx,fminy)
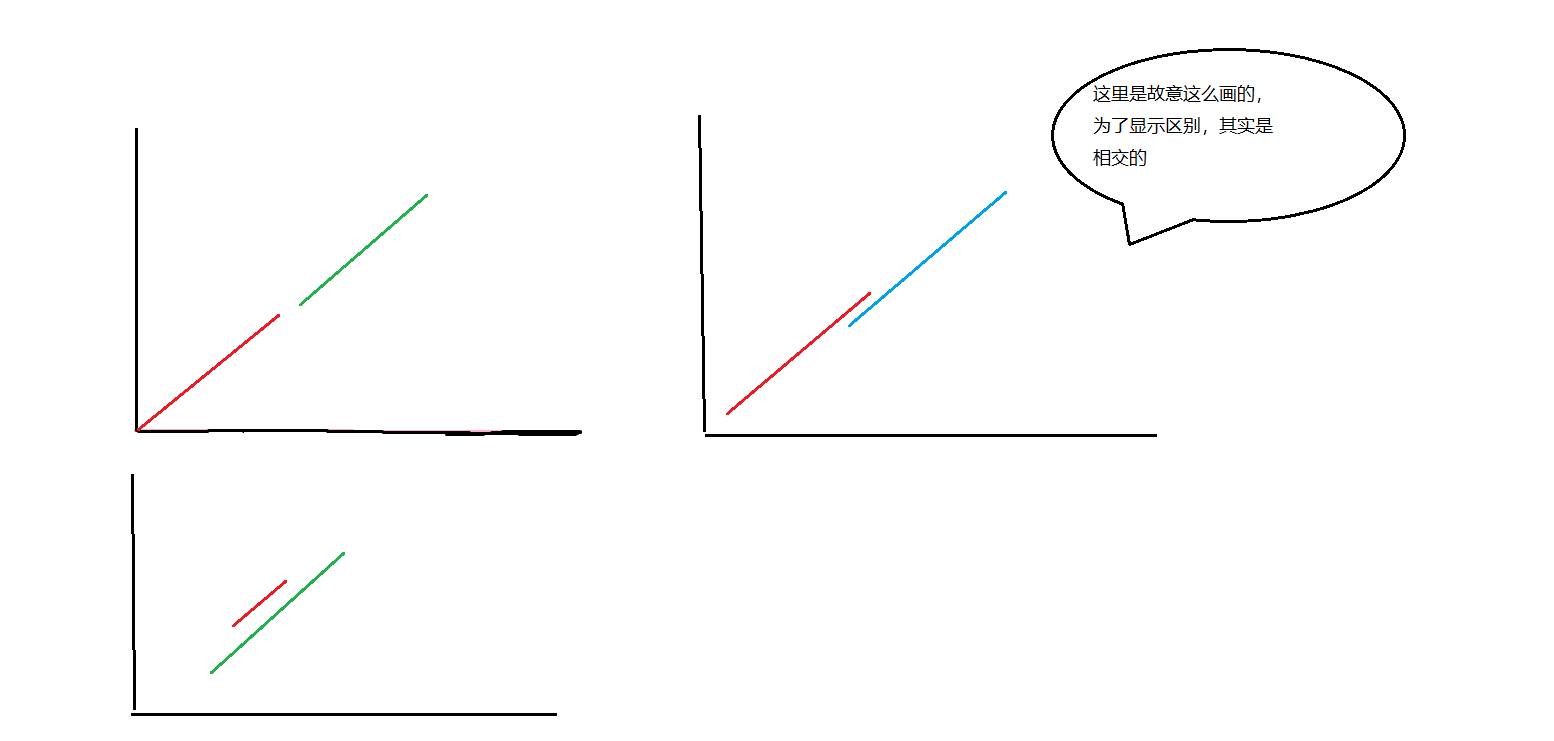
当其中一条为铅垂线，一条为水平线的时候：
- 当水平线的纵坐标小于铅垂线的最小纵坐标或者大于最大纵坐标，肯定无交点
- 当水平线的纵坐标在铅垂线的大小纵坐标之间的时候，如果水平线的左端点小于等于铅垂线的横坐标，右端点大于等于铅垂线的横坐标，则存在交点（铅垂线横坐标，水平线的纵坐标）
最常见的情况，即斜率没什么规律的情况下，这个时候可以直接算出交点，利用简单的数学知识，可以推导出交点 x = (b2 - b1) / (k1 - k2)（b1，b2为两条直线的截距），然后用代入直线算出纵坐标y。之后就是讨论这个交点是否在两条线段之间，即是否在两条线段围出来的图形中。我采用交点到过两端点铅垂线的距离之和是否等于端点距离之和，如果等于说明在范围内，即交点有效，否则无效。

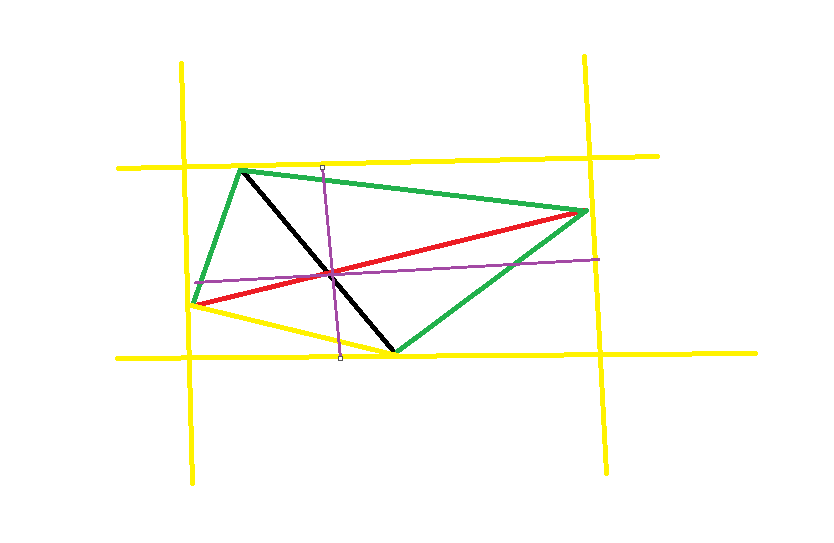
如图所示，红黑两条线段相交，分别判断交点到左右两条黄线和上下两条黄线的距离之和是否直接等于端点的距离。

逻辑分下完了，下面可以写代码了，我这里的代码其实还可以精简，但是目前还没做，仅供参考

def judge(x1,y1,x2,y2,x1_1,y1_1,x2_1,y2_1,x,y):
    # if x1 <= x <= x2 and x1_1 <= x <= x2_1 and y1 <= y <= y2 and y2_1 <= y <= y1_1:
    #     return (x,y)
    xdis1 = abs(x1-x2)
    ydis1 = abs(y1-y2)
    xtox1 = abs(x1-x)
    xtox2 = abs(x-x2)
    ytoy1 = abs(y1-y)
    ytoy2 = abs(y-y2)
    xdis2 = abs(x1_1-x2_1)
    ydis2 = abs(y1_1-y2_1)
    xtox1_1 = abs(x - x1_1)
    xtox2_1 = abs(x - x2_1)
    ytoy1_1 = abs(y - y1_1)
    ytoy2_1 = abs(y - y2_1)
    if xdis1 == (xtox1 + xtox2) and ydis1 == (ytoy1 + ytoy2) \
        and xdis2 == (xtox1_1 + xtox2_1) and ydis2 == (ytoy1_1 + ytoy2_1):
        return (x,y)
    else:
        return []
class Solution:
    def intersection(self, start1: List[int], end1: List[int], start2: List[int], end2: List[int]) -> List[float]:
        
        # 第一条直线
        y1 = start1.pop()
        x1 = start1.pop()
        y2 = end1.pop()
        x2 = end1.pop()
        # 第二条直线
        y1_1 = start2.pop()
        x1_1 = start2.pop()
        y2_1 = end2.pop()
        x2_1 = end2.pop()

        if x1 == x2:
            Y1 = x1
            k1 = float('inf')
        elif y1 == y2:
            Y1 = y1
            k1 = 0
        else:
            k1 = (y2 - y1) / (x2 - x1)
        if x1_1 == x2_1:
            Y1_1 = x1_1
            k2 = float('inf')
        elif y1_1 == y2_1:
            Y1_1 = y1_1
            k2 = 0
        else:
            k2 = (y2_1 - y1_1) / (x2_1 - x1_1)
        b1 = -k1*x1 + y1
        b2 = -k2*x1_1 + y1_1
        if k1 == k2:
            ##两条 铅锤线
            if k1 == float('inf'):
                ##相互平行
                if x1 != x1_1:
                    return []
                else:
                ##判断 两条铅锤线是否有交点
                    fminy = min(y1,y2)
                    fmaxy = max(y1,y2)
                    sminy = min(y1_1,y2_1)
                    smaxy = max(y1_1,y2_1)
                ## 判断两条线谁高一点
                    if fmaxy >= smaxy:
                        if fminy > smaxy:
                            return []
                        else:
                            return (x1,fminy)
                    else:
                        if sminy > fmaxy:
                            return []
                        else:
                            return (x1,sminy)
            ##两条 水平线
            elif k1 == 0:
                ##相互平行
                if y1 != y1_1:
                    return []
                else:
                    ##判断 两条水平线是否有交点
                    fminx = min(x1,x2)
                    fmaxx = max(x1,x2)
                    sminx = min(x1_1,x2_1)
                    smaxx = max(x1_1,x2_1)
                    ##判断哪条长一点
                    if fmaxx >= smaxx:
                        if fminx > smaxx:
                            return []
                        else:
                            return (fminx,y1)
                    else:
                        if sminx > fmaxx:
                            return []
                        else:
                            return (sminx,y1)

                    # if fmaxx < sminx or fminx > smaxx:
                    #     return []
                    # if fmaxx >= sminx:
                    #     return (fmaxx,y1)
                    # if fminx <= smaxx:
                    #     return (x1, fminx)
            ##两条斜线
            else:
                if b1 != b2:
                    return []
                else:
                    if x1 <= x2:
                        fminx = x1
                        #这里实际上不是最小，但是为了区分对应，故意写成这样
                        fminy = y1
                        fmaxx = x2
                        fmaxy = y2
                    else:
                        fminx = x2
                        # 这里实际上不是最小，但是为了区分对应，故意写成这样
                        fminy = y2
                        fmaxx = x1
                        fmaxy = y1

                    if x1_1 <= x2_1:
                        sminx = x1_1
                        #这里实际上不是最小，但是为了区分对应，故意写成这样
                        sminy = y1_1
                        smaxx = x2_1
                        smaxy = y2_1
                    else:
                        sminx = x2_1
                        # 这里实际上不是最小，但是为了区分对应，故意写成这样
                        sminy = y2_1
                        smaxx = x1_1
                        smaxy = y1_1
                    #判断哪条在坐标轴上更偏右
                    if fmaxx >= smaxx:
                        if fminx > smaxx:
                            return []
                        else:
                            if fminx <= sminx:
                                return (sminx,sminy)
                            else:
                                return (fminx,fminy)

                    else:
                        if sminx > fmaxx:
                            return []
                        else:
                            if sminx < fminx:
                                return (fminx,fminy)
                            else:
                                return (sminx,sminy)
                    # if fmaxx < sminx or fminx > smaxx:
                    #     return []
                    # if fmaxx >= sminx:
                    #     return (sminx, sminy)
                    # if fminx <= smaxx:
                    #     return (fminx,fminy)

        if k1 == float('inf') and k2 == 0:
            if y1 <= y2:
                fminy = y1
                fmaxy = y2
            else:
                fminy = y2
                fmaxy = y1
            if x1_1 <= x2_1:
                sminx = x1_1
                smaxx = x2_1
            else:
                sminx = x2_1
                smaxx = x1_1
            if sminx <= x1 and smaxx >= x1 and y2 >= fminy and y2 <= fmaxy:
                return (x1,y2)

        elif k2 == float('inf') and k1 == 0:
            if y1_1 <= y2_1:
                sminy = y1_1
                smaxy = y2_1
            else:
                sminy = y2_1
                smaxy = y1_1
            if x1 <= x2:
                fminx = x1
                fmaxx = x2
            else:
                fminx = x2
                fmaxx = x1
            if fminx <= x1_1 and fmaxx >= x1_1 and y1 >= sminy and y1 <= smaxy:
                return (x2, y1)
        elif k1 == float('inf') and k2 != 0 and k2 != float('inf'):
            y = k2 * x1 + b2
            return judge(x1,y1,x2,y2,x1_1,y1_1,x2_1,y2_1,x1,y)
        elif k2 == float('inf') and k1 !=0 and k1 != float('inf'):
            y = k1 * x1_1 + b1
            return judge(x1, y1, x2, y2, x1_1, y1_1, x2_1, y2_1, x1_1, y)

        x = (b2 - b1) / (k1 - k2)
        y = k1*x + b1

        return judge(x1,y1,x2,y2,x1_1,y1_1,x2_1,y2_1,x,y)

好了，这道题目暂时到这结束，不算很难，但是需要仔细分析。

5.设计一个简化版的推特

你的设计需要支持以下的几个功能：

postTweet(userId, tweetId): 创建一条新的推文
getNewsFeed(userId): 检索最近的十条推文。每个推文都必须是由此用户关注的人或者是用户自己发出的。推文必须按照时间顺序由最近的开始排序。
follow(followerId, followeeId): 关注一个用户
unfollow(followerId, followeeId): 取消关注一个用户

今天的题目比前两天都要简单，没有什么复杂的边界或者数学问题。可以直接利用两个字典来实现。具体分析一下功能

声明两个字典content，star，分别存储用户发的twitter和关注，对应的key都为userid
发推特：
- 利用time模块，记录时间戳，然后与twitterid 封装成 “twitterid-时间戳”的格式存入到content中
- 注意点，由于操作速度很快，可能需要sleep，以此分辨推特的先后顺序
关注用户：
- 先判断userid是否在star中，若不存在，则创建，然后加入对应的id
取关
- 先判断userid是否在star中，若存在，再判断取关对象的id是否在对应的value中，若存在，则移除
获取最近的十条消息
- 先从content中取出用户自己所发推特，如果用户没有关注对象，则直接按顺序返回用户的最近十条推特
- 若用户有关注对象，则取出对象id，然后从content中取出对应的推特（如果该用户发过推特），然后和用户所发推特组成新的列表。接下来遍历该列表。取出对应的value值，利用split得到对应id和时间戳，将其中时间戳最大的的放入结果集中，然后移除该值，进行下轮迭代。如果发现迭代出来的有相同id，则此轮迭代不计数，进行下一轮，总共取到十条记录为止

大致的思路就这样，没有难点，下面就附上代码，仅供参考：

import time
import copy
class Twitter:

    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.star = {}
        self.content={}

    def postTweet(self, userId: int, tweetId: int) -> None:
        """
        Compose a new tweet.
        """
        #运行速度太快。。无法精准计算时间，故休眠
        time.sleep(0.001)
        ticks = time.time()
        if userId not in self.content:
            self.content[userId] = []
            self.content[userId].append(str(tweetId) + '-' + str(ticks))
        else:
            self.content[userId].append(str(tweetId) + '-' + str(ticks))



    def getNewsFeed(self, userId: int):
        """
        Retrieve the 10 most recent tweet ids in the user's news feed. Each item in the news feed must be posted by users who the user followed or by the user herself. Tweets must be ordered from most recent to least recent.
        """
        if userId in self.content:
            mycontent = copy.deepcopy(self.content[userId])
        else:
            mycontent = []
        if userId in self.star:
            followees = copy.deepcopy(self.star[userId])
        else:
            followees = []
        fcontent = []
        res = []
        tweetId = 0
        if followees :
            for id in followees:
                #判断用户是否发过twitter
                if id in self.content:
                    fcontent.extend(self.content[id])

            mycontent.extend(fcontent)
            #print("mycontent",mycontent)
            i=0
            while i <= 9:
                min = float('-inf')
                if mycontent:
                    for val in mycontent:
                        #print(val)
                        tmp = val.split('-')
                        posttime = float(tmp[1])
                        if posttime > min:
                            tweetId = tmp[0]
                            min = posttime
                    if tweetId not in res:
                        res.append(tweetId)
                        i = i + 1

                    mycontent.remove(str(tweetId) + '-' + str(min))

                else:
                    break
            return res
        else:
            for i in range(10):
                if mycontent:
                    id = mycontent.pop().split('-')[0]
                    if id not in res:
                        res.append(id)
                else:
                    break
            return res



    def follow(self, followerId: int, followeeId: int) -> None:
        """
        Follower follows a followee. If the operation is invalid, it should be a no-op.
        """
        if followerId not in self.star:
            self.star[followerId] = []
            self.star[followerId].append(followeeId)
        else:
            self.star[followerId].append(followeeId)

    def unfollow(self, followerId: int, followeeId: int) -> None:
        """
        Follower unfollows a followee. If the operation is invalid, it should be a no-op.
        """
        if followerId in self.star:
            if followeeId in self.star[followerId]:
                self.star[followerId].remove(followeeId)

6.两数相加 II

要求：给你两个非空链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。

你可以假设除了数字 0 之外，这两个数字都不会以零开头。

进阶：

如果输入链表不能修改该如何处理？换句话说，你不能对列表中的节点进行翻转。

要求是很简单的，只要两数和，难点是数字是存放在链表中的，所以我们要写遍历链表，将取出的数字放进列表中。然后判断两个列表的长度，将长的设置为big，另一个叫small,然后在分析：

首先我们在small不为空的条件下，同时对small和big进行pop操作，然后将其相加，再判断是否和大于等于10，若大于等于10，则将结果减去10在将入res，同时将b置为1。否则直接将结果加入res，b置为0
然后在big不为空的情况下，计算big.pop与b的和。在重复条件一后面的判断。这里其实是相加的两个数位数不同的情况下的计算。
最后在big也为空列表的情况下，判断b是否为1，也就是是否存在进位的问题，若为1，则在res中加1。这里是计算20+80这种情况。

最后我们有了结果集res。由于题目要求是返回链表，所以我们遍历结果集，重新生成链表就行了。

下面附上代码：

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:
        arr1 = []
        arr2 = []
        f1 = f2 = True
        while f1:
            arr1.append(l1.val)
            if l1.next != None:
                l1 = l1.next
            else:
                f1 = False
        while f2:
            arr2.append(l2.val)
            if l2.next != None:
                l2 = l2.next
            else:
                f2 = False
        res = []
        if len(arr1) >= len(arr2):
            big = arr1
            small = arr2
        else:
            big = arr2
            small = arr1
        #b为进位数
        b = 0
        while small != []:
            result = big.pop() + small.pop() + b
            if  result >= 10:
                res.insert(0,result-10)
                b = 1
            else:
                res.insert(0,result)
                b = 0

        while big != []:
            result = big.pop() + b
            if  result >= 10 :
                res.insert(0,result-10)
                b = 1
            else:
                res.insert(0,result)
                b = 0

        if big == [] and b == 1:
            res.insert(0,b)

        cache = None
        for i in res:
            tmp = ListNode(i)
            if cache != None:
                cache.next = tmp
                cache = tmp
            else:
                head = ListNode(i)
                cache = head
        return head

7.两数之和

要求：给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那两个整数，并返回他们的数组下标。你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

今天的题目很简单，利用python可以很简单的实现。遍历数组，用target减去当前值，若他们的差在剩余的数组中，则有解，否则进行下一轮迭代。

代码实现

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        i = 0
        length = len(nums)
        while i < length - 1:
            sub = target - nums[i]
            if sub in nums[i + 1:]:
                return (i,i + nums[i + 1:].index(sub)+1)
            i += 1

8.合并区间

要求：给出一个区间的集合，请合并所有重叠的区间。

就是说给出[1,4],[4,5]可以将其合并成[1,5]，即两个区间如果有交集，就可以将他们合并。对于这种问题，我们可以将集合先从小到大排序，然后从头开始比较，分别有以下几种情况

当左区间的右端点小于右区间的左端点时，不能合并
当左区间的右端点大于等于右区间的左端点时，可以合并，但是要分情况：
- 当左区间的左端点A小于右区间的左端点C时，合并后区间的左端点的值为A,否则为C
- 当左区间的右端点B小于右区间的右端点D时，合并后区间的右端点的值为D,否则为B

这样就得到了合并后的区间，我们将其插入到原集合中，并从原集合中删除被合并的区间，进行下一轮迭代。这样到最后就可以得到所有合并后的区间，下面贴上代码

class Solution:
    def merge(self, intervals: List[List[int]]) -> List[List[int]]:
        if intervals == []:
            return []
        row, col = len(intervals), len(intervals[0])
        i = 0
        intervals.sort()
        while i + 1 < row:
            if intervals[i][col - 1] >= intervals[i + 1][0]:
                tmp1 = intervals[i]
                tmp2 = intervals[i + 1]
                mergearr = []
                if intervals[i][0] <= intervals[i + 1][0]:
                    mergearr.append(intervals[i][0])
                else:
                    mergearr.append(intervals[i + 1][0])
                if intervals[i][col - 1] >= intervals[i + 1][col - 1]:
                    mergearr.append(intervals[i][col - 1])
                else:
                    mergearr.append(intervals[i + 1][col - 1])
                intervals.remove(tmp1)
                intervals.remove(tmp2)
                intervals.insert(0, mergearr)
                row = len(intervals)
                i = 0
                intervals.sort()
            else:
                i += 1
        return intervals

9.跳跃游戏

要求：给定一个非负整数数组，你最初位于数组的第一个位置。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个位置。

今天的题目，用官方提供的贪心算法来解决。因为我用的是递归方法，并且用到了全局变量，导致在跑测试用例时不准确，等之后调整好了在提供我的思路。现在先来看一下官方的：

设想一下，对于数组中的任意一个位置 $y$ ，我们如何判断它是否可以到达？根据题目的描述，只要存在一个位置 $x$ ，它本身可以到达，并且它跳跃的最大长度为 $x + \textit{nums}[x]$ ，这个值大于等于 $y$ ，即 $x + \textit{nums}[x] \geq y$ ，那么位置 $y$ 也可以到达。

换句话说，对于每一个可以到达的位置 $x$ ，它使得 $x+1, x+2, \cdots, x+\textit{nums}[x]$ 这些连续的位置都可以到达。

这样以来，我们依次遍历数组中的每一个位置，并实时维护最远可以到达的位置。对于当前遍历到的位置 $x$ ，如果它在最远可以到达的位置的范围内，那么我们就可以从起点通过若干次跳跃到达该位置，因此我们可以用 $x + \textit{nums}[x]$ 更新最远可以到达的位置。

在遍历的过程中，如果最远可以到达的位置大于等于数组中的最后一个位置，那就说明最后一个位置可达，我们就可以直接返回 True 作为答案。反之，如果在遍历结束后，最后一个位置仍然不可达，我们就返回 False 作为答案。

以题目中的示例一

[2, 3, 1, 1, 4]
为例：

我们一开始在位置 0，可以跳跃的最大长度为 2，因此最远可以到达的位置被更新为 2；

我们遍历到位置 1，由于 $1 \leq 2$ ，因此位置 1 可达。我们用 11加上它可以跳跃的最大长度 3，将最远可以到达的位置更新为 4。由于 4大于等于最后一个位置 4，因此我们直接返回 True。

我们再来看看题目中的示例二

[3, 2, 1, 0, 4]
我们一开始在位置 0，可以跳跃的最大长度为 3，因此最远可以到达的位置被更新为 3；

我们遍历到位置 1，由于 $1 \leq 3$ ，因此位置 1可达，加上它可以跳跃的最大长度 2 得到 3，没有超过最远可以到达的位置；

位置 2、位置 3 同理，最远可以到达的位置不会被更新；

我们遍历到位置 4，由于 4 > 3，因此位置 4 不可达，我们也就不考虑它可以跳跃的最大长度了。

在遍历完成之后，位置 4 仍然不可达，因此我们返回 False.

class Solution:
    def canJump(self, nums: List[int]) -> bool:
        n, rightmost = len(nums), 0
        for i in range(n):
            if i <= rightmost:
                rightmost = max(rightmost, i + nums[i])
                if rightmost >= n - 1:
                    return True
        return False

10.整数反转

描述：给出一个 32 位的有符号整数，你需要将这个整数中每位上的数字进行反转。注意:

假设我们的环境只能存储得下 32 位的有符号整数，则其数值范围为 [ $-2^{31},2^{31}-1$ ]。请根据这个假设，如果反转后整数溢出那么就返回 0。

这道题有很多解法，这里采用了字符串的方法.

先判断是否为0 若为0，直接返回0
先判断正负号，如果是负数，先转换为整数
若为整数，将数字转化为字符串在遍历，拼接字符串：
- 在转换为int类型。判断范围，不在范围内返回0
- 若刚才的为负数，返回的时候添加负号

下面是代码：

def reversestr(x):
    s=''
    for tmp in str(x):
        s = tmp + s
    x = int(s)
    if x < -2**31 or x >  2**31-1:
        return 0
    else:
        return x
class Solution:
    def reverse(self, x: int) -> int:
        if x == 0:
            return 0 
        elif x < 0:
            x = -x
            return -reversestr(x)
        else:
            return reversestr(x)

11.两个栈实现队列

描述：用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

这道题目是很挺简单的。因为python的列表可以很方便的实现。

- 题目要求队尾插入整数，可以用append

- 队头实现删除功能，所以利用pop

附上代码

class CQueue:

    def __init__(self):
        self.queue = []

    def appendTail(self, value: int) -> None:
        self.queue.append(value)

    def deleteHead(self) -> int:
        if self.queue:
            return self.queue.pop(0)
        return -1


# Your CQueue object will be instantiated and called as such:
# obj = CQueue()
# obj.appendTail(value)
# param_2 = obj.deleteHead()

12.斐波那契数列

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项。斐波那契数列的定义如下：

F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

这个题目很简单，直接递归就行了。但是要注意的是，这里用到了一个装饰器—-lru_cache。因为这里面需要大量的重复计算。而lru_cache能把相对耗时的函数结果进行保存，避免传入相同的参数重复计算。

from functools import lru_cache
class Solution:
    @lru_cache(None)
    def fib(self, n: int) -> int:
        if n < 2:
            return n
        return (self.fib(n-1) + self.fib(n-2))%1000000007

13.青蛙跳台阶问题

描述：一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

这题依旧可以看做是斐波那契数列，但是需要注意起始条件不同。当n=0时，应该返回1.另一种方法就是动态规划。

状态定义：设 dp 为一维数组，其中 dp[i] 的值代表斐波那契数列第 $i$ 个数字。
dp[i + 1] = dp[i] + dp[i - 1]dp[i+1]=dp[i]+dp[i−1] ，即对应数列定义 f(n + 1) = f(n) + f(n - 1)f(n+1)=f(n)+f(n−1)
初始状态： dp[0] = 1 dp[1] = 1，即初始化前两个数字；
返回值： dp[n] ，即斐波那契数列的第 n 个数字。

class Solution:
    def numWays(self, n: int) -> int:
        a, b = 1, 1
        for _ in range(n):
            a, b = b, a + b
        return a % 1000000007

14.最小栈

描述：设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

push(x) —— 将元素 x 推入栈中。
pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。

这道题很简单，就不多说了，直接上代码：

class MinStack:

    def __init__(self):
        """
        initialize your data structure here.
        """
        self.s = []
        self.min = float('inf')

    def push(self, x: int) -> None:
        self.s.append(x)
        if x < self.min:
            self.min = x

    def pop(self) -> None:
        if self.s:
            self.s.pop()

        
    def top(self) -> int:
        if self.s:
            return self.s[-1]

    def getMin(self) -> int:
        if self.s:
            return min(self.s)



# Your MinStack object will be instantiated and called as such:
# obj = MinStack()
# obj.push(x)
# obj.pop()
# param_3 = obj.top()
# param_4 = obj.getMin()

15.层次遍历

描述：给你一个二叉树，请你返回其按 层序遍历 得到的节点值。（即逐层地，从左到右访问所有节点）

示例：
二叉树：[3,9,20,null,null,15,7],

/ \
9 20
/ \
15 7
返回其层次遍历结果：

[
[3],
[9,20],
[15,7]
]

解题思路

只要遍历二叉树同时记录对应节点的位置就行了

遍历二叉树，记录节点值，同时记录位置

当二叉树左子树不为空，位置加一，递归
当二叉树右子树不为空，且左子树为空，位置加一，递归
遍历过程中，不要重复追加[]就可以了

代码：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    res = [[]]
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root :
            return []
        self.res = [[]]
        self.dfs(root,0) 
        return self.res
    def dfs(self,root,pos):
        if not root:
            return
        self.res[pos].append(root.val)
        if root.left != None:
            pos += 1
            #判断该层节点值是否已经开始记录
            if len(self.res) < pos+1:
                self.res.append([])
            self.dfs(root.left,pos)
        if root.right != None:
            if root.left == None:
                pos += 1
                #判断该层节点值是否已经开始记录
                if len(self.res) < pos+1:
                    self.res.append([])
            self.dfs(root.right,pos)
        return self.res

16.只出现一次的数字

描述：给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素

说明：

你的算法应该具有线性时间复杂度。你可以不使用额外空间来实现吗

解题思路

首先想到的是利用哈希，但是需要额外空间。然后还有一种是暴力法，两次for循环，找出。最后一种是看了官方题解，采用异或的方法：

既满足时间复杂度又满足空间复杂度，就要提到位运算中的异或运算 XOR，主要因为异或运算有以下几个特点：

一个数和 0 做 XOR 运算等于本身：a⊕0 = a
一个数和其本身做 XOR 运算等于 0：a⊕a = 0
XOR 运算满足交换律和结合律：a⊕b⊕a = (a⊕a)⊕b = 0⊕b = b
故而在以上的基础条件上，将所有数字按照顺序做抑或运算，最后剩下的结果即为唯一的数字
时间复杂度：O(n)，空间复杂度：O(1)

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        tmp = 0
        for i in range(len(nums)):
            tmp ^= nums[i]
        return tmp

17.设计哈希集合

描述：不使用任何内建的哈希表库设计一个哈希集合（HashSet）。

实现 MyHashSet 类：

void add(key) 向哈希集合中插入值 key 。
bool contains(key) 返回哈希集合中是否存在这个值 key 。
void remove(key) 将给定值 key 从哈希集合中删除。如果哈希集合中没有这个值，什么也不做。

说明：

解题思路

因为用的python3，所以可以采用集合或者列表来实现。非常简单的一道题。

class MyHashSet:

    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.map =  set()


    def add(self, key: int) -> None:
        if not key in self.map:
            self.map.add(key)

    def remove(self, key: int) -> None:
        if key in self.map:
            self.map.discard(key)

    def contains(self, key: int) -> bool:
        """
        Returns true if this set contains the specified element
        """
        if key in self.map:
            return True
        return False

18.只出现一次的数字 II

描述：给你一个整数数组 nums ，除某个元素仅出现一次外，其余每个元素都恰出现 三次。请你找出并返回那个只出现了一次的元素。

进阶：你的算法应该具有线性时间复杂度。你可以不使用额外空间来实现吗？

解题思路

1.利用map 这种方法很简单，不多说

class Solution:
     def singleNumber(self, nums: List[int]) -> int:
         map = {}
         for i in nums:
             if i not in map:
                 map[i] = 0
             else:
                 map[i] += 1
         for k,v in map.items():
             if v == 0:
                 return k

2.利用指针。先将数组排序。然后判断当前指针的左右数值是否相等，则可以找出只出现一次的数字。注意一下指针的范围以及一种特殊情况就行

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        nums.sort()
        if len(nums) == 1:
            return nums[0]
        elif nums[0] != nums[1]:
            return nums[0]
        for i in range(1,len(nums)-1):
            if nums[i] != nums[i-1] and nums[i] != nums[i+1]:
                return nums[i]
            elif nums[i] != nums[i+1] and i+1 == len(nums)-1:
                return nums[i+1]

19.有效的括号

描述：给定一个只包括 ‘(‘，’)’，’{‘，’}’，’[‘，’]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。

解题思路

利用栈后进先出的特点，可以很简单的做出来，不多做赘述。

class Solution:
    kuohao = {
        ')':'(',
        ']':'[',
        '}':'{'
    }
    def isValid(self, s: str) -> bool:
        stack = []
        if len(s) <= 1:
            return False
        for i in s :
            if i == '(' or i =='[' or i == '{':
                stack.append(i)
            else:
                if len(stack) == 0:
                    return False
                left = stack.pop()
                if self.kuohao[i] != left:
                    return False
        if len(stack) == 0:
            return True
        else:
            return False

20.整数转罗马数字

描述：

罗马数字包含以下七种字符： I， V， X， L，C，D 和 M。

字符	数值
I	1
V	5
X	10
L	50
C	100
D	500
M	1000

例如，罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。
给定一个整数，将其转为罗马数字。输入确保在 1 到 3999 的范围内。

解题思路

我们用最直白的方法来处理，首先将数字对1000取整，例如2345，对1000取整可以得到2，也就是千位的数字q。然后将原数减去q*1000得到345。再重复这个过程直到个位数处理。只要注意几个特殊罗马数字就行。

class Solution:
    def intToRoman(self, num: int) -> str:
        res = ''
        q = num // 1000
        if q > 0:
            num -= q * 1000
            for x in range(q):
                res += 'M'

        b = num // 100
        if b == 9 :
            num -= 900
            res += 'CM'
        elif b >= 5:
            num -= b * 100
            res += 'D'
            for x in range(b-5):
                res += 'C'
        elif b == 4:
            num -= 400
            res += 'CD'
        
        elif b > 0 :
            num -= b * 100
            for x in range(b):
                res += 'C'

        s = num // 10
        if s == 9 :
            num -= 90
            res += 'XC'
        elif s >= 5:
            num -= s * 10
            res += 'L'
            for x in range(s-5):
                res += 'X'
        elif s == 4:
            num -= 40
            res += 'XL'
        elif s > 0 :
            num -= s * 10
            for x in range(s):
                res += 'X'
        if num == 9:
            res += 'IX'
        elif num >= 5:
            res += 'V'
            for x in range(num-5):
                res += 'I'
        elif num == 4:
                res += 'IV'
        elif num > 0:
            for x in range(num):
                res += 'I'
        return res

21. 反转链表

描述：定义一个函数，输入一个链表的头节点，反转该链表并输出反转后链表的头节点。

示例:

输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

解题思路

题目要求反转列表，所以用头插法，只需要遍历一遍原列表，则可以完成要求。所谓头插法，就是新建一个空的头结点H，然后遍历原链表，每次遍历新生成一个临时节点temp，将遍历中的结点值赋给temp，再将temp的next指向h，再把h指向temp，这样构造出来的链表就是原链表的逆向。

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        h = None
        while head is not None:
            temp = ListNode()
            temp.val = head.val
            temp.next = h
            h = temp
            head = head.next
        return h

C语言版本

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */


struct ListNode* reverseList(struct ListNode* head){
    struct ListNode* L = (struct ListNode*)malloc(sizeof(struct ListNode));
    struct ListNode* node;
    L->next = NULL;
    while(head != NULL){
        node = (struct ListNode*)malloc(sizeof(struct ListNode));
        node->val = head->val;
        node->next = L->next;
        L->next = node;
        head = head->next;
    }
    return L->next;
}

22.罗马数字转整数

描述: 给定一个罗马数字，将其转换成整数。输入确保在 1 到 3999 的范围内。

可以参考20题的描述.

解题思路
对于罗马数字转整数，本质就是加法和减法。通过特例可以发现，当左边数字a比右边数字b小的时候，做减法也就是b-a,其余情况都是加法且最后一位一定是加法。所以只需遍历字符串，且用当前指针与下一位作比较，若做减法则指针+2,否则右移一位直至遍历结束.

class Solution:
    map = {
        "I":1,"V":5,"X":10,"L":50,"C":100,"D":500,"M":1000,"IX":9
    }
    def romanToInt(self, s: str) -> int:
        res = i = 0
        l = len(s)
        while i + 1 < l:
            if self.map[s[i]] < self.map[s[i+1]]:
                res -= self.map[s[i]]
                res += self.map[s[i+1]]
                i += 2
            else:
                res += self.map[s[i]]
                i += 1
                
        if i == l - 1:
            res += self.map[s[l-1]]
        return res

23. 2的幂

描述：给定一个整数，编写一个函数来判断它是否是 2 的幂次方。

解题思路

最暴力简单的思路，显然，能被2整除到1的数字一定是 2 的幂次方，故一直除2，直到等于1返回true，若小于1则False

class Solution:
    def isPowerOfTwo(self, n: int) -> bool:
        if n == 1:
            return True
        elif n > 1:
            return self.isPowerOfTwo(n/2)
        else:
            return False

24.添加与搜索单词 - 数据结构设计

描述：请你设计一个数据结构，支持添加新单词和查找字符串是否与任何先前添加的字符串匹配。

实现词典类 WordDictionary ：

WordDictionary() 初始化词典对象
void addWord(word) 将 word 添加到数据结构中，之后可以对它进行匹配
bool search(word) 如果数据结构中存在字符串与 word 匹配，则返回 true ；否则，返回 false 。word 中可能包含一些 ‘.’ ，每个 . 都可以表示任何一个字母。

解题思路

初始化数组用来保存新单词同时增加一个字典，用来防止重复添加。
搜索时，先判断搜索词是否在key中，如果有直接返回True，否则进行遍历。
对于map中的每个单词，若长度与搜索词的长度不同，则直接返回False。否则进行逐个判断，若相等或搜索词中包含’.’，则i++
若i最终与搜索词长度相等，说明搜索成功并将该搜索词添加到key中，否则搜索失败！

class WordDictionary:

    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.map = []
        self.key = {}

    def addWord(self, word: str) -> None:
        if word not in self.key:
            self.map.append(word)
            self.key[word] = True

    def search(self, word: str) -> bool:
        if word in self.key:
            return True
        length = len(word)
        for val in self.map:
            if length != len(val):
                continue
            i = 0
            while i < length:
                if word[i] == val[i] or word[i] == '.':
                    i += 1
                else:
                    break
            if i == length:
                self.key[word] = True
                return True
        return False

25.相同的树

描述：给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

解题思路

这是一道简单题，判断两棵树是否相同，可以直接用DFS实现。首先当p，q值不等时，一定不是两颗相同的树，或者其中一颗树为Null，另一棵树不为null，说明两棵树也不想等。只有当两棵树同时为null的时候，它们一定相同。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
        if not p and not q:
            return True
        elif not p or not q:
            return False
        elif p.val != q.val:
            return False
        else:
            return self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)

26.二叉树的最大深度

描述：给定一个二叉树，找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

解题思路

对于求深度问题，可以从DFS或者BFS来入手。对于DFS来说，若根结点为空，则直接返回0，否则直接递归左右子树，若左子树高度大于右子树，就返回左子树高度+1，否则返回右子树高度+1

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        lhigh = self.maxDepth(root.left)
        rhigh = self.maxDepth(root.right)
        if (lhigh > rhigh):
            return lhigh + 1
        else:
            return rhigh + 1

27.二叉树的中序遍历

描述：给定一个二叉树的根节点 root ，返回它的中序遍历。

解题思路

很简单，只需要递归遍历即可，喜欢的使用迭代也行。对于中序来说，显然是LNR，所以先遍历左子树，为空的时候返回，同时加入结点值，然后遍历右子树

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorder(self,root,res):
        if not root:
            return
        self.inorder(root.left,res)
        res.append(root.val)
        self.inorder(root.right,res)
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        res = []
        self.inorder(root,res)
        return res

28.两数相加

描述：给你两个非空的链表，表示两个非负的整数。它们每位数字都是按照逆序的方式存储的，并且每个节点只能存储一位数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

解题思路

首先，更改一下常规加法的思维惯性。对于该题加法，我们默认从左向右加，并且向右进位。例如243+564，2+5=7， 4+6=10向右进1，则3+4+1=8，即243+564=708
故，对于两个链表非空时遍历，初始进位标志c=0：

l1，l2非空，直接两个链表值和c相加，同时指针后移，并判断是否需要进位，若有进位需将c置为1
若l1,或l2为空，则将值置为0，重复1步骤的过程
循环结束后，由于末尾也有可能进位，所以最后需要对c校验，若为1，则需将该值加入到链表尾部。

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:
        a = b = c = 0
        p = head = ListNode()
        while l1 or l2:
            node = ListNode()
            if l1:
                a = l1.val
                l1 = l1.next
            else:
                a = 0
            if l2 :
                b = l2.val
                l2 = l2.next
            else:
                b = 0
            if a + b + c > 9:
                node.val = a + b + c - 10
                c = 1
            else:
                node.val = a + b + c
                c = 0  
                
            p.next = node
            p = node
        if c == 1:
            p.next = ListNode(1)
        
        return head.next
。

29.4的幂

描述：给定一个整数，写一个函数来判断它是否是 4 的幂次方。如果是，返回 true ；否则，返回 false 。

整数 n 是 4 的幂次方需满足：存在整数 x 使得 n == 4x

解题思路

判断是不是4的幂，只要判断这个数是否能被4一直除到1即可：

整除到1，返回true
小于1，返回false

class Solution:
    def isPowerOfFour(self, n: int) -> bool:
        if n == 1:
            return True
        elif n < 1:
            return False
        else:
            return self.isPowerOfFour(n/4)

30. 山脉数组的峰顶索引

描述：符合下列属性的数组 arr 称为山脉数组：
arr.length >= 3
存在 i（0 < i < arr.length - 1）使得：
arr[0] < arr[1] < … arr[i-1] < arr[i]
arr[i] > arr[i+1] > … > arr[arr.length - 1]
给你由整数组成的山脉数组 arr ，返回任何满足 arr[0] < arr[1] < … arr[i - 1] < arr[i] > arr[i + 1] > … > arr[arr.length - 1] 的下标 i 。

解题思路

按照要求，最简单的方法是遍历，当找到满足arr[i] < arr[i+1] > arr[i+2]就可以了。

class Solution:
    def peakIndexInMountainArray(self, arr: List[int]) -> int:
        length = len(arr)
        i = 0
        while i < length - 2:
            if arr[i] < arr[i+1] and arr[i+1] > arr[i+2]:
                return i+1
            i += 1

31.雪糕的最大数量

描述：夏日炎炎，小男孩 Tony 想买一些雪糕消消暑。

商店中新到 n 支雪糕，用长度为 n 的数组 costs 表示雪糕的定价，其中 costs[i] 表示第 i 支雪糕的现金价格。Tony 一共有 coins 现金可以用于消费，他想要买尽可能多的雪糕。

给你价格数组 costs 和现金量 coins ，请你计算并返回 Tony 用 coins 现金能够买到的雪糕的最大数量。

注意：Tony 可以按任意顺序购买雪糕。

解题思路

按照题目需要求，最容易想到的就是先排序，然后用贪心算法。因为需要购买最多的雪糕，所以自然先买价格低的，知道买不起为止。所以我们对数组排序后，逐一比较价格即可

class Solution:
    def maxIceCream(self, costs: List[int], coins: int) -> int:
        costs.sort()
        if coins < costs[0]:
            return 0
        count = 1
        coins -= costs[0]
        for val in costs[1:]:
            if coins < val:
                return count
            else:
                count += 1
                coins -= val
        return count

32.根据字符出现频率排序

描述：给定一个字符串，请将字符串里的字符按照出现的频率降序排列。

解题思路

这道题目，思路就是遍历字符串，然后按频率重新拼接字符串就可以了。

最简单的方式就是用map一一记录。然后在根据map重新拼接。

class Solution:
    def frequencySort(self, s: str) -> str:
        map = {}
        for val in s:
            if val not in map:
                map[val] = 1
            else:
                map[val] += 1
        map = dict(sorted(map.items(),key=lambda x:x[1],reverse=True))
        str = ''
        for key in map:
            i = 0
            length = map[key]
            while i < length:
                str += key
                i += 1
        return str

33.点菜展示表

描述:

给你一个数组 orders，表示客户在餐厅中完成的订单，确切地说， orders[i]=[customerNamei,tableNumberi,foodItemi] ，其中 customerNamei 是客户的姓名，tableNumberi 是客户所在餐桌的桌号，而 foodItemi 是客户点的餐品名称。

请你返回该餐厅的点菜展示表。在这张表中，表中第一行为标题，其第一列为餐桌桌号 “Table” ，后面每一列都是按字母顺序排列的餐品名称。接下来每一行中的项则表示每张餐桌订购的相应餐品数量，第一列应当填对应的桌号，后面依次填写下单的餐品数量。

注意：客户姓名不是点菜展示表的一部分。此外，表中的数据行应该按餐桌桌号升序排列。

解题思路

对于题目要求，显然只要保存桌号与对应菜品的关系即可，然后菜单第一行单独列出即可

首先遍历菜单，利用字典，将桌号作为key，对应菜品(数组)作为value保存
题目要求桌号升序排列，所以利用sorted对字典key排序
对于menu，利用set去重然后在sorted排序得到升序的菜单列表
最后按照key的顺序，首先加入桌号，然后遍历菜单，与map中保存的菜品对比计数就可以

class Solution:
    def displayTable(self, orders: List[List[str]]) -> List[List[str]]:
        map = {}
        menu = []
        for arr in orders:
            num = int(arr[1])
            menu += arr[2:]
            if num not in map:
                map[num] = arr[2:]
            else:
                map[num].extend(arr[2:])
        key = sorted(map)
        menu = sorted(set(menu))
        res = []
        menu.insert(0,'Table')
        res.append(menu)
        for num in key:
            temp = []
            temp.append(str(num))
            for val in menu[1:]:
                temp.append(str(map[num].count(val)))
            res.append(temp)
        return res

34.斐波那契数

描述：斐波那契数，通常用 F(n) 表示，形成的序列称为斐波那契数列。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给你 n ，请计算 F(n) 。

解题思路

这里非常容易想到用递归的方式，也可以用动态规划，这里先用递归，下一题使用动态规划。很容易看出递归出口为n=0和n=1，其他情况直接返回 F(n - 1) + F(n - 2)

class Solution:
    def fib(self, n: int) -> int:
        if n <= 1:
            return n
        return self.fib(n-1) + self.fib(n-2)

35.第 N 个泰波那契数

描述：泰波那契序列 Tn 定义如下：

T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2

给你整数 n，请返回第 n 个泰波那契数 Tn 的值。

解题思路

这题用动态规划的思路来解决：

第一步先确定dp数组的含义，dp[i]就代表第i个泰波那契数。然后初始化，所以dp[0] = 0,dp[1] = 1,dp[2] = 1
第二步写出递推关系式: dp[n+3] = dp[n+1] + dp[n+2]
第三步确定遍历顺序，从第二步可以知道，先要求出dp[n-1]，才能求的dp[n],所以是从dp[0]开始往后求

所以这道题目就很简单，只需要求出dp数组就可以，但是实际上我们不需要维护这样一个数组，我们只需维护dp[n],dp[n+1],dp[n+2]就可以，所以利用四个变量a，b，c，sum。首先sum = a+b+c ,然后a=b，b=c，c=sum，这样就ok

class Solution:
    def tribonacci(self, n: int) -> int:
        if n == 0:
            return 0
        elif n <= 2:
            return 1
        a,b,c,d = 0,1,1,0
        for i in range(2,n):
            d = a + b + c
            a = b
            b = c
            c = d
        return d

36.使用最小花费爬楼梯

描述:

数组的每个下标作为一个阶梯，第 i 个阶梯对应着一个非负数的体力花费值 cost[i]（下标从 0 开始）。

每当你爬上一个阶梯你都要花费对应的体力值，一旦支付了相应的体力值，你就可以选择向上爬一个阶梯或者爬两个阶梯。

请你找出达到楼层顶部的最低花费。在开始时，你可以选择从下标为 0 或 1 的元素作为初始阶梯。

解题思路

首先这题要明白，离开阶梯 i 需要花费cost[i]的体力，此时你会到达i+1或者i+2层阶梯。接下来：

确定dp数组的含义，显然dp[i]代表到达第i层的体力花费。
初始化dp数组，题目中说可以选择从下标为 0 或 1 的元素作为初始阶梯，所以很显然dp[0] = dp[1] = 0
推导状态转移方程，到达第二层楼梯可以从第0层走两步到达，或者从第一层走一步，所以dp[2] = min(dp[0]+cost[0],dp[1] + cost[1]),同理，到达第i层，dp[i] = min(dp[i-2]+cost[i-2],dp[i-1] + cost[i-1])

由此我们得到了一个dp数组，dp[n]就是我们所求答案。但是其实并不需要维护一整个数组，可以使用动态数组的思想，只维护dp[i-1]和dp[i-2]。

class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        if len(cost) == 2:return min(cost)
        a = b = 0
        n = len(cost)
        for i in range(2, n + 1):
            c = min(b + cost[i - 1], a + cost[i - 2])
            a, b = b, c
        return b

37.打家劫舍I

描述:

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你不触动警报装置的情况下，一夜之内能够偷窃到的最高金额。

解题思路

首先对于动态规划题目，先要明确dp数组的含义以及初始化，然后在确定状态转移方程。对于本题目，要求抢劫最多的钱，所以dp数组应该代表抢劫最多的钱，那么很显然dp[i]就代表有\i+1**家给你抢，然后你不被发现的情况下获得最多的钱。那么接下来初始化dp数组:

dp[0] 显然就是num[0]，也就是只有一家给你抢劫，你别无选择只能含泪抢她
dp[1] 显然是num[0]和num[1]中的最大值，也就是有两家给你抢劫，你肯定抢钱多的那家

接下来分析一下i>=2的情况：

当i=2时，有三家a,b,c欢迎你抢劫，那么在不被发现的情况下，你有两种选择方式，要么抢劫ac，要么抢b，也就是说dp[2] = max(a+c,b)。而a就是dp[0],c就是nums[2],b就是dp[1]，也即dp[2] = max(dp[0]+nums[2],dp[1])
当i=3时，有四家a,b,c,d欢迎你抢劫，和i=2时一样，你有两种选择方式，要么抢劫ac，要么抢bd，同理，dp[3] = max(a+c,b+d),此时d=nums[3],这里重点是:若a+c>b+d那么a+c>b,所以a+c=dp[2],若a+c<b,那么a+c<b+d并且b<b+d,故a+c仍然可以替换成dp[2]不影响结果，也即dp[3] = max(dp[2]),dp[1]+nums[3])
综上，i=n时,状态转移方程：dp[n] = max(dp[n-1],dp[n-2]+nums[n])

到此，代码已经可以直接写出来了，得到一个dp数组，最后的值就是所求值。由转移方程可知，其实只需要维护dp[n-1]和dp[n-2]即可，所以可以利用滚动数组优化存储空间。用a代表dp[0],b代表dp[1],那么dp[2] = max(a + nums[2],b),再将dp[1]赋值给a,dp[2]赋值给b,再求dp[3],重复赋值操作一直往下就可以咯。

class Solution:
    def rob(self, nums: List[int]) -> int:
        n = len(nums)
        if n == 1:return nums[0]
        if n == 2:return max(nums)
        a = nums[0]
        b = max(nums[0:2])
        for i in range(2,n):
            sum = max(a + nums[i],b)
            a = b
            b = sum
        return b
# class Solution:
#     def rob(self, nums: List[int]) -> int:
#         n = len(nums)
#         if n == 1:return nums[0]
#         if n == 2:return max(nums)
#         dp = [0] * n
#         dp[0] = nums[0]
#         dp[1] = max(nums[0:2])
#         for i in range(2,n):
#             dp[i] = max(dp[i-2] + nums[i],dp[i-1])

#         return dp[-1]

38.打家劫舍 II

描述：

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，今晚能够偷窃到的最高金额。

解题思路

这题与第一题的唯一的区别就是首尾算相邻，所以要么有头没尾，要么有尾没头，就相当于是两个不同区间的动态规划，然后取其中最大值。剩下的就与第一种抢劫一毛一样了。具体可以参考上一题.

class Solution:
    def rob(self, nums: List[int]) -> int:
        def robYou(arr):
            n = len(arr)
            a = arr[0]
            b = max(arr[0:2])
            for i in range(2,n):
                sum = max(a + arr[i],b)
                a = b
                b = sum
            return b
        n = len(nums)
        if n == 1:return nums[0]
        if n == 2:return max(nums)
        return max(robYou(nums[0:n-1]),robYou(nums[1:]))

39.删除并获得点数

描述：

给你一个整数数组 nums ，你可以对它进行一些操作。每次操作中，选择任意一个 nums[i] ，删除它并获得 nums[i] 的点数。之后，你必须删除所有等于 nums[i] - 1 和 nums[i] + 1 的元素。开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。

解题思路

聪明的强盗又来了。。。首先题目中说，选择了值为A元素后，所有A+1和A-1的元素都不能选择，所以这里其实就是邻居的意思。也就是说，A,A+1,A-1是邻居，不能连着偷。所以我们只需要重新生成一个数组，此题就转换成打家劫舍I了。转换规则就是，原数组中的值转换为新数组的下标，而新数组对应的值为原数组的值乘以个数。这样该题就可以解决了。

class Solution:
    def deleteAndEarn(self, nums: List[int]) -> int:
        n = len(nums)
        if n == 1: return nums[0]
        new = [0] * (max(nums) + 1)
        for i in nums:
            if new[i] == 0:
                new[i] = i * nums.count(i)
        a = new[0]
        b = max(new[0:2])
        for i in range(2,len(new)):
            sum = max(a + new[i],b)
            a = b
            b = sum
        return b

40 .跳跃游戏

描述：

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

解题思路
要判断是否能到达最后一个下标，首先设最大距离max_distance为0，max_distance为当前能够到达的最远距离，那么只有两种情况：

若当前下标加上对应距离和大于数组长度减1，则代表可以到达末尾，返回True
若当前下标大于max_distance，则直接返回False

class Solution:
    def canJump(self, nums: List[int]) -> bool:
        max_distance = 0
        n = len(nums) - 1
        for i,v in enumerate(nums):
            if i > max_distance : return False
            if i + v >= n : return True
            max_distance = max(max_distance,i + v)

41.最大子序和

描述：

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

解题思路

对于长度为一的数组，我们直接返回就可以了，那么当数组长度大于二的时候，如何考虑呢？首先默认数组第一位为最大值p，那么接下来长度为2时，最大值要么是p+nums[1]，要么是nums[1]，依次类推，有递推公式dp[i]=max{dp(i−1)+nums[i],nums[i]}

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        n = len(nums)
        if n == 1: return nums[0]
        p = maxsum = nums[0]
        for i in range(1,n):
            p = max(nums[i], p + nums[i])
            maxsum = max(p,maxsum)
        return maxsum

41.剑指 Offer 58 - II. 左旋转字符串

描述：

字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如，输入字符串”abcdefg”和数字2，该函数将返回左旋转两位得到的结果”cdefgab”。

解题思路

利用python3的字符串运算符，可以直接得到答案：
在python中，对于一个字符串可以任意截取长度

## s='abc'
## s[0:2] = 'a'
## 左闭右开
class Solution:
    def reverseLeftWords(self, s: str, n: int) -> str:
        return s[n:len(s)] + s[0:n]

42.剑指 Offer 53 - I. 在排序数组中查找数字 I

描述：

统计一个数字在排序数组中出现的次数。

解题思路

index()方法语法：
list.index(x[, start[, end]])

参数
x— 查找的对象。
start— 可选，查找的起始位置。
end— 可选，查找的结束位置。
返回值
该方法返回查找对象的索引位置，如果没有找到对象则抛出异常。
数组又是升序的，所以再往后比较即可

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        try:
            i = nums.index(target)
        except:
            return 0
        count = 1
        for v in nums[i+1:]:
            if v == target:
                count += 1
                continue
            break

        return count

43.剑指 Offer 32 - II. 从上到下打印二叉树 II

描述：

从上到下按层打印二叉树，同一层的节点按从左到右的顺序打印，每一层打印到一行。

例如:
给定二叉树: [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7
返回其层次遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

解题思路

显然，这题最容易想到就是BFS,但是答案中要求的是同层次的在一个列表中，所以这时候需要控制一下循环。具体思路如下：

首先若root为None,直接返回 []
若不为空，则用一个队列将根节点入队，同时设置一个变量，用来记录每层的节点数量，初始值为1
在队列不空的情况下，根节点出队列，同时设置两个变量c和count，c用来记录当前循环次数，count用来记录下层节点个数

具体代码：

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root: return []
        res = []
        queue = []
        num = 1
        queue.append(root)
        while queue:
            temp = []
            c = count = 0
            while c < num:
                node = queue.pop(0)
                temp.append(node.val)
                if node.left: 
                    queue.append(node.left)
                    count += 1
                if node.right: 
                    queue.append(node.right)
                    count += 1
                c += 1
            num = count
            res.append(temp)
        return res

44.剑指 Offer 32 - III. 从上到下打印二叉树 III

描述：

请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。

例如:
给定二叉树: [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7
返回其层次遍历结果：

[
  [3],
  [20,9],
  [15,7]
]

解题思路

这题的关键在于每层的输出顺序相反，本质依旧是BFS，只需要根据层数，判断是从左到右还是从右到左输出即可。

首先若root为None,直接返回 []
若不为空，则用一个队列将根节点入队，同时设置一个变量，用来记录每层的节点数量，初始值为1
在队列不空的情况下，根节点出队列，同时设置两个变量c和count，c用来记录当前循环次数，count用来记录下层节点个数，用level来记录当前层数，若为奇数层（根节点为第一层），从左到右，否则从右向左。

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root: return []
        res = []
        queue = []
        num = level = 1
        queue.append(root)
        while queue:
            temp = []
            c = count = 0
            while c < num:
                node = queue.pop(0)
                temp.append(node.val)
                if node.left: 
                    queue.append(node.left)
                    count += 1
                if node.right: 
                    queue.append(node.right)
                    count += 1
                c += 1
            num = count
            level += 1
            if level % 2 != 0:
                temp.reverse()
            res.append(temp)
        return res

45.剑指 Offer 63. 股票的最大利润

描述：假设把某股票的价格按照时间先后顺序存储在数组中，请问买卖该股票一次可能获得的最大利润是多少？

解题思路

首先题目中说的是一次买卖，所以最大利润肯定是某段时间内的最大值减最小值，所以设dp[i]代表前i日的最大利润，那么后一日的最大利润要么是dp[i]，要么是后一日的价格减去前i日中最小值，所以有dp[i]=max(dp[i-1],today_price - minprice),接下来确定边界值。首先第一日利润肯定为0，所以dp[0] = 0。接下来优化一下存储空间，我们只需要保存最大利润maxprofit就可以，minprice用来存放最低价格。

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        minprice = float('inf')
        maxprofit = 0
        for price in prices:
            maxprofit = max(price - minprice, maxprofit)
            minprice = min(price, minprice)
        return maxprofit

46.剑指 Offer 47. 礼物的最大价值

描述：

在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

示例：

输入: 
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物

解题思路

首先，对于棋盘中每一个格，它只能由左→右，上→下，所以可以设dp[i,j]代表从棋盘的起点（左上角）走到第(i,j)格子的最大价格，所以可以很容易得到状态转移方程：dp[i,j] = max(dp[i-1,j],dp[i,j-1]) + grid[i,j]。接下来需要讨论边界情况：

$i=0,j=0，\quad dp[0,0] = grid[0,0]$

$i=0，j\not= 0,\quad dp[0,j] = dp[0,j-1] + grid[0,j]$
$i\not=0，j= 0,\quad dp[i,0] = dp[i-1,0] + grid[i,0]$
$i\not=0,j\not=0, dp[i,j] = max(dp[i-1,j],dp[i,j-1]) + grid[i,j]$

同时，可以先将i=0和j=0的情况拿出来单独运算，避免循环中的冗余判断。

class Solution:
    def maxValue(self, grid: List[List[int]]) -> int:
        row, col = len(grid), len(grid[0])
        for j in range(1,col):
            grid[0][j] += grid[0][j-1]
        for i in range(1,row):
            grid[i][0] += grid[i-1][0]
        for i in range(1,row):
            for j in range(1,col):
                grid[i][j] += max(grid[i-1][j],grid[i][j-1])

        return grid[-1][-1]

47.剑指 Offer 46. 把数字翻译成字符串

解题思路

对于长度为1的数字，显然只有一种翻译方法，长度为2的数字可能是一种也可能是两种翻译方法，这就对应了跳一个台阶还是两个台阶的青蛙问题，唯一的区别在于跳两个台阶时存在限制条件。对此，进行以下分析：

用s代表字符串，dp[i]代表长度为i的数字的翻译方法，则有

dp[1] = 1
对于dp[2],若s[0:2] > 25,dp[2] = 1, 否则dp[2] = 2.

初始条件确定了以后，基本可以按照跳台阶的思路来：

若 9 < s[i-1:i+1] <= 25 dp[i] = dp[i-2] + dp[i-1],否则 dp[i] = dp[i-1]

最后利用循环数组优化空间就可以了

class Solution:

    def translateNum(self, num) :
        if num < 10: return 1
        s = str(num)
        if len(s) == 2:
            if num > 25:
                return 1
            return 2

        a, b, c = 1, 0, 0
        b = a if int(s[0:2]) > 25 else a + 1

        for i in range(2,len(s)):
            t = int(s[i-1:i+1])
            c = a + b if t <= 25 and t > 9 else b
            a = b
            b = c

        return c

力扣每日一题（力扣官网）

1.数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合

2.给定一个字符串，逐个翻转字符串中的每个单词。

3.鸡蛋掉落

4.交点

5.设计一个简化版的推特

6.两数相加 II

7.两数之和

8.合并区间

9.跳跃游戏

10.整数反转

11.两个栈实现队列

12.斐波那契数列

13.青蛙跳台阶问题

14.最小栈

15.层次遍历

16.只出现一次的数字

17.设计哈希集合

18.只出现一次的数字 II

19.有效的括号

20.整数转罗马数字

21. 反转链表

22.罗马数字转整数

23. 2的幂

24.添加与搜索单词 - 数据结构设计

25.相同的树

26.二叉树的最大深度

27.二叉树的中序遍历

28.两数相加

29.4的幂

30. 山脉数组的峰顶索引

31.雪糕的最大数量

32.根据字符出现频率排序

33.点菜展示表

34.斐波那契数

35.第 N 个泰波那契数

36.使用最小花费爬楼梯

37.打家劫舍I

38.打家劫舍 II

39.删除并获得点数

40 .跳跃游戏

41.最大子序和

41.剑指 Offer 58 - II. 左旋转字符串

42.剑指 Offer 53 - I. 在排序数组中查找数字 I

43.剑指 Offer 32 - II. 从上到下打印二叉树 II

44.剑指 Offer 32 - III. 从上到下打印二叉树 III

45.剑指 Offer 63. 股票的最大利润

46.剑指 Offer 47. 礼物的最大价值

47.剑指 Offer 46. 把数字翻译成字符串

1.数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且有效的括号组合