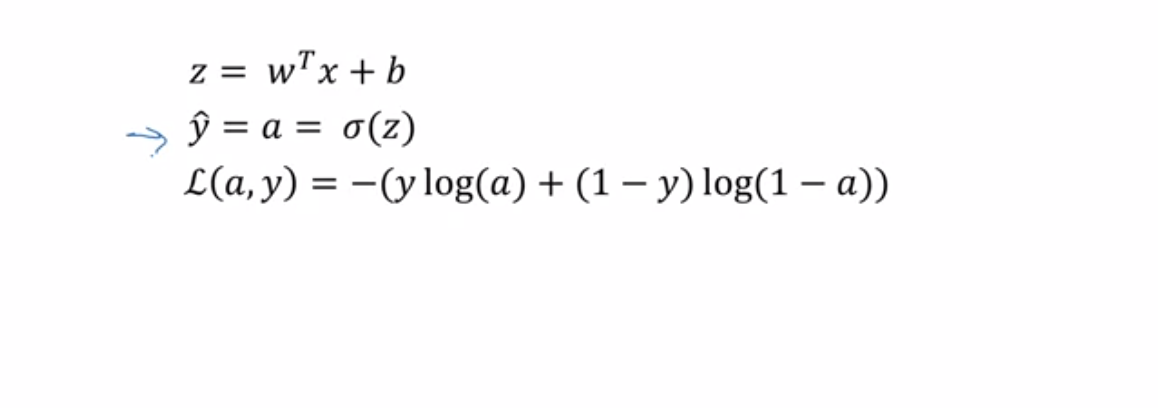neural-networks-deep-learning-week2

[Deep Learning]将逻辑回归模型作为神经网络

最近开始学习吴恩达的deeplearning课程，从第二周开始，会开始介绍关于逻辑回归模型的一些简单定义，在这里开始做一些简单的笔记，用以后面的复习。

• 预测输出

$$\hat{y} = sigmoid(w^{T} + b)$$ $$sigmoid = \frac{1}{1 + e^{-z}}$$

• 损失函数（Loss）：

  对于线性回归中：

  $$L = \left(\dfrac{1}{2}\right) (\hat{y} - y)^{2}$$

  而在逻辑回归中，损失函数被定义为：

  $$L = -(ylog(\hat{y}) + (1-y)log(1-\hat{y}))$$

  具体而言，可以这么理解 yhat：

  即在给定x的情况下 y等于1的概率为多少

  $$\hat{y} = p(y=1|x)$$

也就是说

如果 y=1

$$p(y|x) = \hat{y}$$

如果 y=0

$$p(y|x) = 1 - \hat{y}$$

将两种情况写在一起 即为 （将y=0 y=1 代入 可以得到与上面相同的公式）

$$p(y|x) = \hat{y}^{y}(1 - \hat{y})^{1 - y}$$

又由于log函数为单调增函数，故取对数

$$log\left(p(y|x)\right) = ylog(\hat{y}) + (1-y)log(1-\hat{y}) = -L$$

注意这里的负号，因为在逻辑回归中，我们想最大化概率，所以就需要最小化损失函数。

• 代价函数（COST）

  在m个样本中的代价可以定义为

  $$log(p) = log\prod_{i=1}^m p(y^\left(i\right)|x^\left(i\right)) = \sum_{i=1}^m log\left(p(y^\left(i\right)|x^\left(i\right))\right) = -\sum_{i=1}^m L(\hat{y}^\left(i\right),y^\left(i\right))$$

  （在统计学中，有一种最大似然估计的方法，即选择使式子最大化的参数。）

  则有

  $$J(w,b) =\frac{1}{m}\sum_{i=1}^m L(\hat{y}^\left(i\right),y^\left(i\right))$$

  因为这里要求最小值，故不需要这个负号(1/m 为缩放系数，只是为了最后的数值能在更好的尺度上，没有其他特殊含义)

• 梯度下降

  在逻辑回归中，我们有以下的定义：

  

  对其求偏导数（链式求导，如果不熟悉，可以看宇哥的十八讲~）

  $$\frac{dL}{da} = -\frac{y}{a} + \frac{1-y}{1-a}$$

$$\frac{da}{dz} =-(1+e^{-z})^{-2} * -e^{-z} = e^{-z}*(1+e^{-z})^{-2} = a*(1-a)$$

注：

$$e^{-z}*(1+e^{-z})^{-2} = \frac{e^{-z}}{(1+e^{-z})^{2}} = \frac{1+e^{-z}-1}{(1+e^{-z})^{2}} = \frac{1}{1+e^{-z}} - \frac{1}{(1+e^{-z})^{2}} = a-a^2=a(1-a)$$

则有

$$\frac{dL}{dz} = \frac{dL}{da} * \frac{da}{dz} =(-\frac{y}{a} + \frac{1-y}{1-a}) * a(1-a)=a-y$$

同样的

$$\frac{dL}{dw_1} = x_1*dz$$

在计算出这些导数后，就可以进行梯度下降了

$$w_1 = w_1 - \alpha*dw_1$$ $$w_2 = w_2 - \alpha*dw_2$$ $$b = b -\alpha*db$$

---

以上就是对第二周的小小整理（没有对向量化的部分以及numpy的使用做总结，关于numpy的使用会单独写），具体来说，这门课和之前的机器学习中讲的略有不同，比如记号之类的地方，但是大体而言还是差不多的，加油加油！