neural-networks-deep-learning-week3

[Deep Learning] 浅层神经网络

• 理解隐藏层和隐藏单元
• 能够使用多种类型的激活函数
• 用隐藏层建立一个前向传播和反向传播算法
• 应用随机初始化

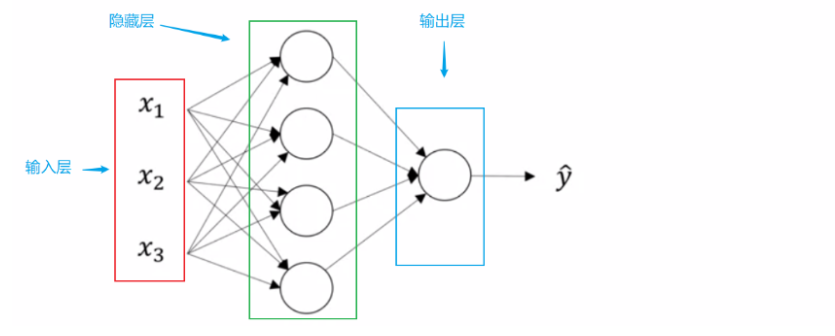
浅层神经网络结构

• 单样本前向传播

  首先，看一下神经网络的结构图

  

这是一个两层的神经网络（输入层不算做一层，认为是第0层）。一般用 X 代表输入，也可以用$a^{[0]}$ 表示 （a代 表激活的意思），用$a^{[1]}$代表第一层即隐藏层，$a^{[2]}$代表输出层。所以上图中 ，X =$a^{[0]}$$\in R^{3}$ ,$a^{[1]} \in R^{4}$,$a^{[2]}\in R$ 。 现在来看隐藏层第一个节点即$a^{[1]}_{1}$的计算，这个计算和逻辑回归一样。首先算出

$$z^{[1]}_1 = w^{[1]T}_1x + b^{[1]}_1$$

然后计算

$$a^{[1]}_1 = sigmoid(z^{[1]}_1)$$

其他节点 同理计算，整理一下

$$z^{[1]}_1 = w^{[1]T}_1x + b^{[1]}_1,a^{[1]}_1 = sigmoid(z^{[1]}_1)$$ $$z^{[1]}_2 = w^{[1]T}_2x + b^{[1]}_2,a^{[1]}_2=sigmoid(z^{[1]}_1)$$ $$z^{[1]}_3 = w^{[1]T}_3x + b^{[1]}_3,a^{[1]}_3=sigmoid(z^{[1]}_3)$$ $$z^{[1]}_4 = w^{[1]T}_4x + b^{[1]}_4,a^{[1]}_4=sigmoid(z^{[1]}_4)$$

• 前向传播向量化

  接下来将这几个式子向量化

$$\left[ \begin{matrix} --w^{[1]T}_1-- \\ --w^{[1]T}_2-- \\ --w^{[1]T}_3-- \\ --w^{[1]T}_4-- \end{matrix} \right] * \left[ \begin{matrix} x_1 \\ x_2 \\ x_3 \end{matrix} \right] + \left[ \begin{matrix} b^{1}_1 \\ b^{1}_2 \\ b^{1}_3 \\ b^{1}_4 \end{matrix} \right] = \left[ \begin{matrix} w^{[1]T}_1x + b^{[1]}_1 \\ w^{[1]T}_2x + b^{[1]}_2 \\ w^{[1]T}_3x + b^{[1]}_3 \\ w^{[1]T}_4x + b^{[1]}_4 \end{matrix} \right] = \left[ \begin{matrix} z^{[1]}_1 \\ z^{[1]}_2 \\ z^{[1]}_3 \\ z^{[1]}_4 \\ \end{matrix} \right]$$

​ 第一个矩阵为4 x 3的矩阵 ,这是因为$w^{1}_l$都属于 三维列向量，现在将他们的转置竖直拼 接为新的矩阵，所以维度4x3。简化一下，可以得到下面的公式

$$z^{[1]} = W^{[1]} x + b^{[1]}$$ $$a^{[1]} = sigmoid(z^{[1]})$$ $$z^{[2]} = W^{[2]}a^{[1]} + b^{[2]}$$ $$a^{[2]} = sigmoid(z^{[2]})$$

​ 因为 x 可以写作$a^{[0]}$,所以

$$z^{[1]} = W^{[1]} a^{[0]} + b^{[1]}$$

​ 其中，$W^{[1]} \in R^{4*3},b\in R^{4*1}, W^{[2]}\in R^{1*4},b^{[2]} \in R$,所以最后$a^{[2]}$ 也是一个实数。

​ 到此，就完成了一个实例的神经网络计算。

• 多样本前向传播

接下来 讨论一下对于多个样本的计算：

首先解释一下符号的意思， 第i个样本第k层的节点定义为$a^{[k](i)}$。

则在计算m个样本的时候，需要像下面这样计算

for i = 1 to m:

$$z^{[1](i)} = W^{[1]} x^{(i)} + b^{[1]}$$ $$a^{[1](i)} = sigmoid(z^{[1](i)})$$ $$z^{[2](i)} = W^{[2]}a^{[1](i)} + b^{[2]}$$ $$a^{[2](i)} = sigmoid(z^{[2](i)})$$

• 多样本前向传播向量化

  首先将多个x样本水平拼接为X，维度为 n x m ，即

$$X = \left[ \begin{matrix} | & | & | \\ x^{(1)} & x^{(2)} & x^{(3)} \\ | & | & | \\ \end{matrix} \tag{n * m} \right]$$

则 向量化 如下

$$Z^{[1]} = W^{[1]} X + b^{[1]}$$ $$A^{[1]} = sigmoid(Z^{[1]})$$ $$Z^{[2]} = W^{[2]} A^{[1]} + b^{[2]}$$ $$A^{[2]} = sigmoid(Z^{[2]})$$

同样的 ，$Z^{[1]}$ ，$A^{[1]}$都是矩阵。到此就已经全部完成了。

激活函数

• sigmoid函数

  目前为止，我们使用的激活函数一直都是sigmoid。它的图像是这样：

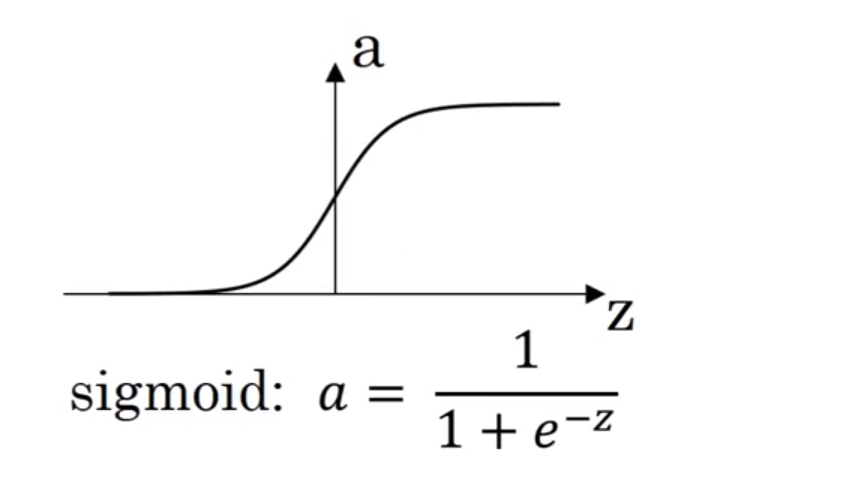
可以看到，当z非常大或者非常小的时候，它斜率也非常小，这样会使梯度下降很慢。所以基本上不会使用这个激活函数。 除非在做二元分类的时候，需要输出值在o-1之间,只有在这个时候会在输出层选择它。需要注意的是，对于隐藏层和输出层来讲，可以选择不同的激活函数。

• tanh函数

  一般情况下，tanh函数都要优于sigmoid函数，它的图像如下：

  

  它的公式为：

$$tanh = \frac{e^{z} - e^{-z}}{e^{z} + e^{-z}}$$

其实是sigmoid函数经过变换后得来的。尽管他的表现要比sigmoid函数要好，但是仍旧面临同样的问题，就是当z过大或过小的时候，斜率非常小。所以也不怎么使用它。

• ReLU函数（线性修正单元）

  它的公式为 ReLU = max(0,z) , 图像长这样：

  

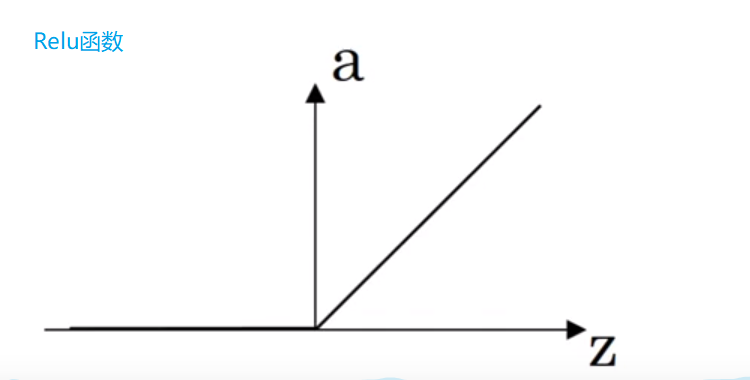
所以只要z为正数，那么斜率就一直为1，z为负数时，斜率为0。虽然当z=0时，导数无定义（左导数和右导数不相等），但是在实际编程时，遇到z=0的概率非常非常小，并且也可以通过指定z=0时，导数为0或者1，所以不用纠结这个问题。

所以一般情况下都用ReLU，或者在你不知道使用哪种激活函数时，就选择它。就比如我们在做二元分类的问题时，可以将所有隐藏层的激活函数都设置为ReLU，然后将输出层的激活函数设置为sigmoid。

此外 ，ReLU函数还有另一种版本。

• Leaky ReLU（带泄露的ReLU）

它的公式为 ReLU = max(0.01z,z) , 图像长这样：

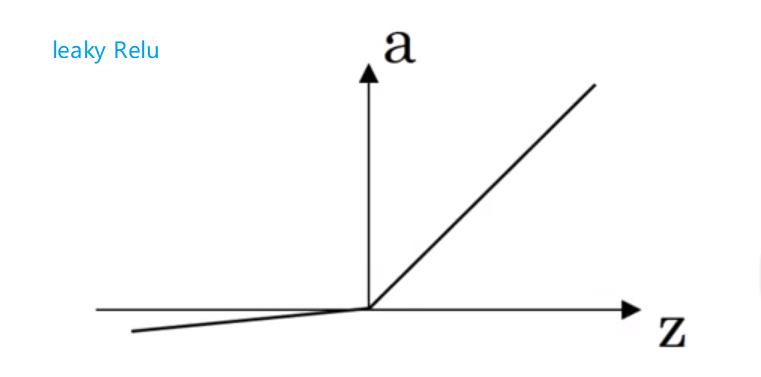
当z为负数时，它的斜率不在为0，而是一个轻微的倾斜。这种激活函数实际上使用起来和ReLU没什么太大的区别，具体可以看个人爱好，或者在你的模型中，将两种都尝试一下，来试试效果。

顺带说一句，因为在NN中，有足够多的隐藏单元来使得z为正数，所以在使用ReLU的时候也不用太担心梯度下降的问题。

激活函数求导

• sigmoid

  关于它的求导，可以参考上一篇博客：neural-networks-deep-learning-week2

  这里就不再赘述。

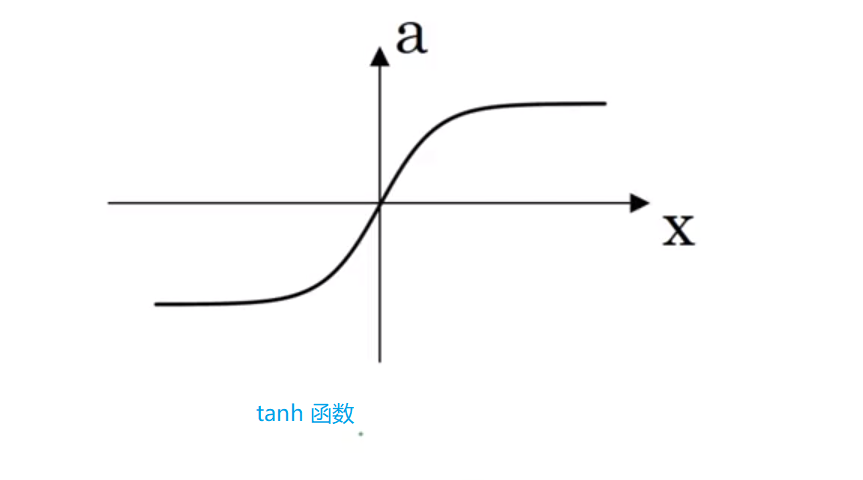
• tanh 函数

  首先，有它的公式

  $$g(z) = tanh(z) = \frac{e^{z} - e^{-z}}{e^{z} + e^{-z}}$$

则有

$$g^{'}（z） = 1 - (tanh(z))^{2}$$

具体求导过程可以自行求导，不是很难

• ReLU函数

  $$g(z) = max(0,z)$$

  求导非常简单

  $$g^{'}(z) = \left\{ \begin{aligned} 1 & &if && z\geq0 \\ 0 & &if && z<0 \end{aligned} \right.$$

  当z=0时，我们手动设置导数为0或者1（在数学中这是不可以的，==该点不可导==）

神经网络中的梯度下降

现在需要讨论 在NN 中如何进行梯度下降，假设目前还是做得二元分类问题且只包含一层隐藏层，那么我们有损失函数的定义如下：

$$J(w^{[1]},b^{[1]},w^{[2]},b^{[2]}) =\frac{1}{m}\sum_{i=1}^m L(\hat{y}^\left(i\right),y^\left(i\right)) \\ 其中 ，n_x=n^{[0]}为特征的个数，n^{[1]}为隐藏单元个数，n^{[2]}为输出单元个数\\ w^{[1]}的维度 为 n^{[1]} * n^{[0]}，b^{[1]}是一个n^{[1]}维向量，即n^{[1]}*1 \\ w^{[1]}的维度 为 n^{[2]} * n^{[1]}，b^{[2]}是一个n^{[2]}维向量，即n^{[2]}*1$$

• 梯度下降的做法就是用 变量 减去 学习率与对应偏导数的乘积

$$\begin{array}\\ Repeat\{\\ dw^{[1]} = \frac{\partial J}{\partial w^{[1]}}, db^{[1]} = \frac{\partial J}{\partial b^{[1]}} …… \\ w^{[1]} = w^{[1]} - \alpha * dw^{[1]},b^{[1]} = b^{[1]} - \alpha * db^{[1]},……\\ \} \end{array}$$

• 反向传播

  具体的过程为（向量化）：

$$\begin{array} dZ^{[2]} = A^{[2]} - Y \\ dW^{[2]} = \frac{1}{m}dZ^{[2]} * A^{[1]T} \\ db^{[2]} = \frac{1}{m}np.sum(dZ^{[2]},axis=1,keepdims=True)\\ axis=1为水平方向，keepdims=True防止输出秩为一的矩阵即(n,)这种形式 \\ dZ^{[1]} = W^{[2]T} dZ^{[2]} .* g^{[1]'}(Z^{[1]}) \\ dW^{[1]} = \frac{1}{m} dZ^{[1]}X^{T}\\ db^{[1]} = \frac{1}{m}np.sum(dZ^{[1]},axis=1,keepdims=True)\\ \end{array}$$ （ .* 代表逐个元素相乘 ）

整个过程就是这样，如果不是很明白，可以去B站搜一搜，有很多推导过程，由于时间所限，这里就不一一推导。

随机初始化

在逻辑回归中，将权重参数全部初始化为0这是可以的，但是在NN中这是不行的。我们来看一看这是为什么。

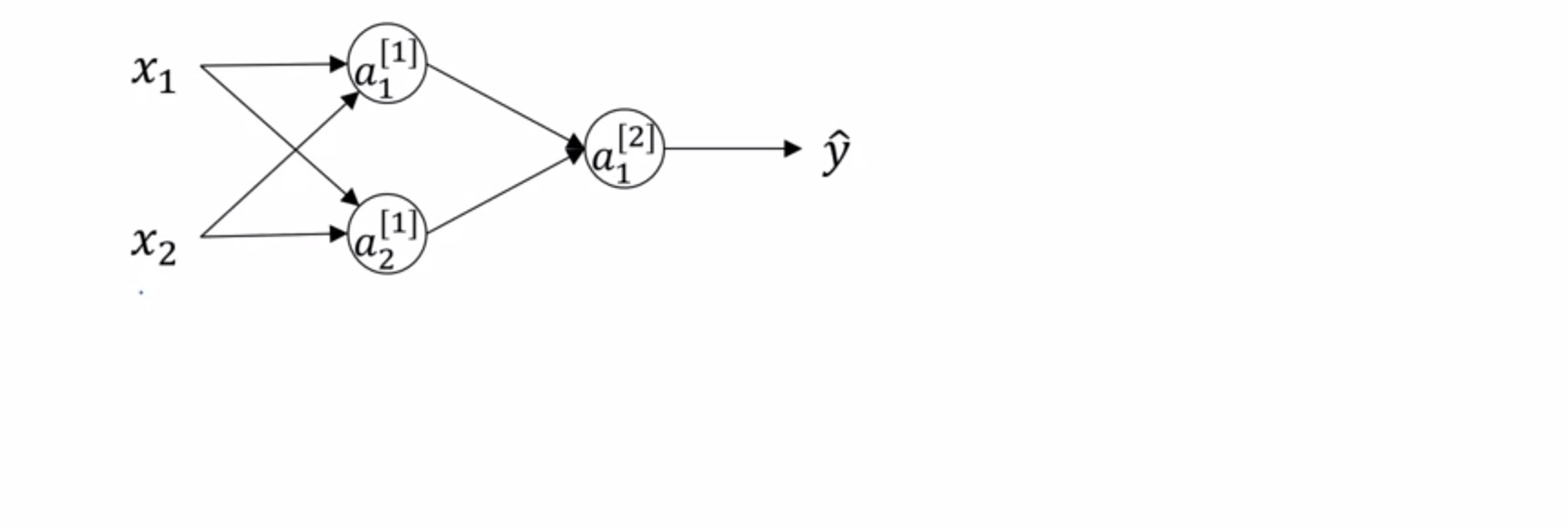
在上图中，有两个输入即$n^{[0]} =2$, 隐藏层有两个单元即$n^{[1]} =2$,那么$W^{[1]}$是一个2x2的矩阵，$b^{[1]}$是一个2x1的矩阵。而这会导致无论输入是什么，总有$a^{[1]}_1 =$$a^{[1]}_2$。当进行反向传播的时候，由于对称问题，会导致$dz^{[1]}_1$ =$dz^{[1]}_2$

……

因此，如果全部初始化为0的话，所以的隐藏单元实际上都是相同的，无论训练多久，它们始终相同。推广到多个隐藏层，隐藏单元也依旧成立。所以需要随机初始化。

---

本周内容相对而言稍微难一点，主要是反向传播中的链式求导，不太熟的可以去看看链式求导法则。最好是要搞懂原理，不然在之后的多层网络中会比较难以理解