neural-networks-deep-learning-week4

[Deep Learning] 深层神经网络

本周目标：

• 将深层神经网络视为一个接一个的连续块

• 建立和训练深层L层神经网络

• 分析矩阵和向量维数以检查神经网络的实现。

• 了解如何使用缓存将信息从正向传播传递到反向传播。

• 了解超参数在深度学习中的作用

---

块的思想

• 对于每层的计算，可以将其视为一个块，如下图

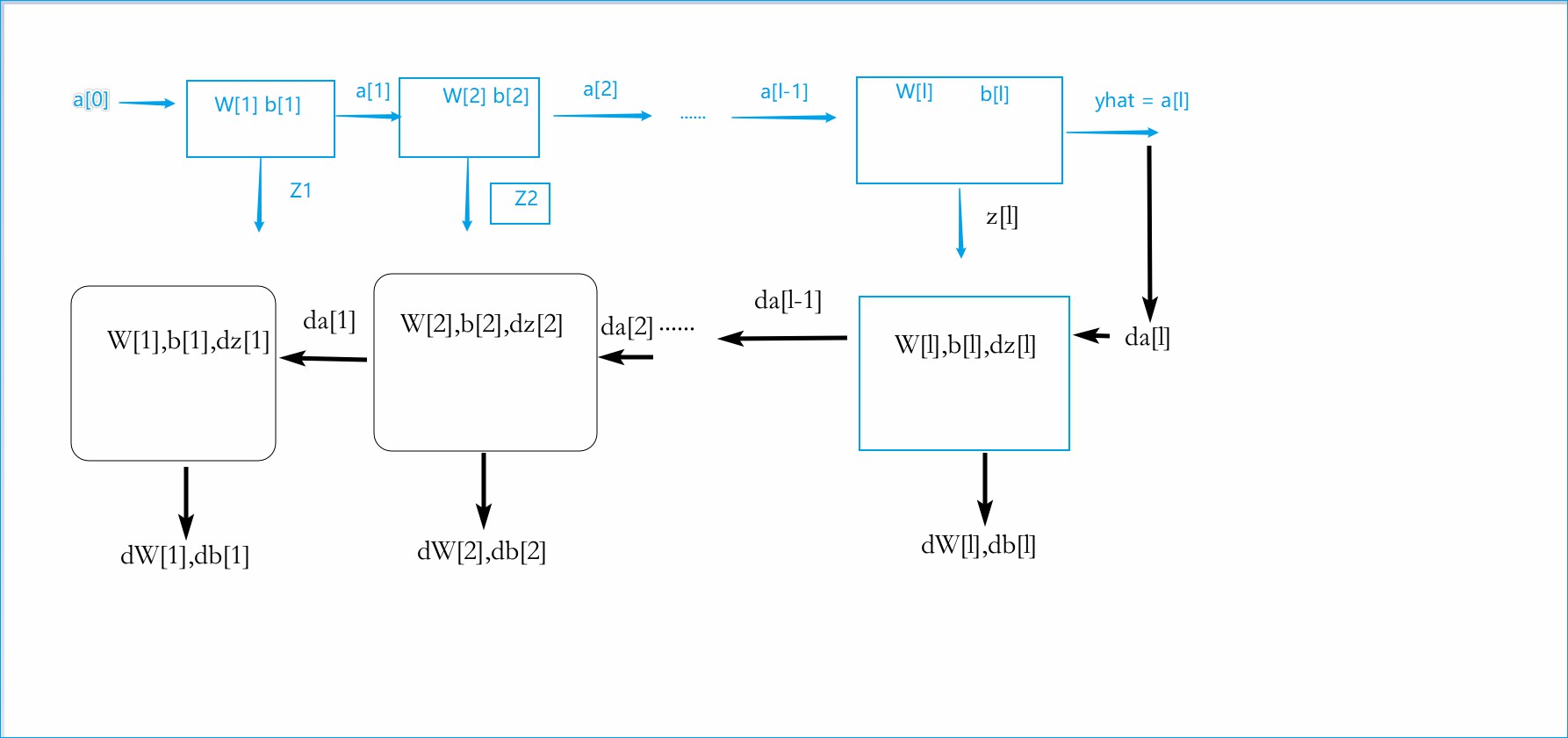
对于此图，只需要理解其过程即可，在前向传播过程中，将变量Z1,Z2等等存储起来，然后在反向传播过程中，就可以很方便地使用他们。

检查矩阵维度

• 在写代码过程中，检查各个参数的维度，能有效的避免一些奇怪的BUG。用下图举个栗子

  

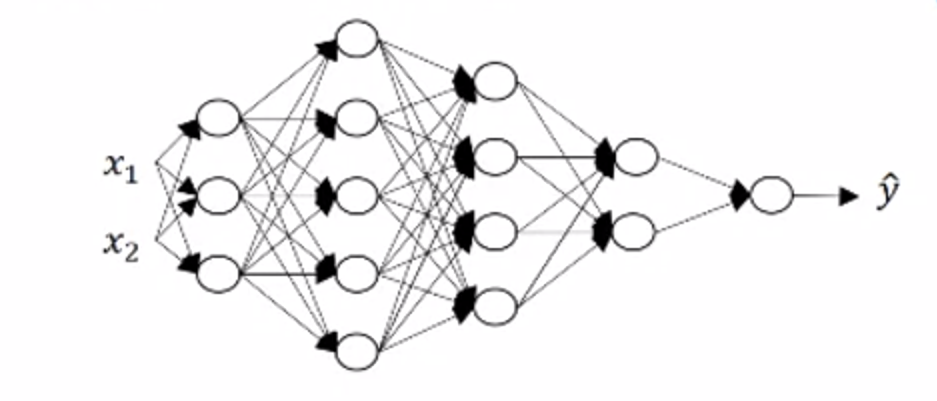
  如图所示，这是一个五层的神经网络，有参数$W^{[1]},b^{[1]}...$ 首先，先确定$W^{[1]}$的维度，可以看到，第一个隐藏层有三个单元，即$n^{[1]} = 3$ ,而输入为$x_1,x_2$，即$n^{[0]}=n_x=2$,可以看做是一个 2 x 1的列向量。又有$z^{[1]} = W^{[1]}x + b^{[1]}$,先忽略$b^{[1]}$，我们已经知道$z^{[1]}$是 3 x 1 的列向量，那么根据线性代数的有关知识，可以直接推断出$W^{[1]}$是 3 x 2 的矩阵。（若有 A矩阵 的维度为 m x k ,B矩阵的维度为 k x n,那么 AB矩阵相乘得到的矩阵C的维度为 m x n）。那$b^{[1]}$的矩阵维度为 3 x 1。同理，我们可以推断出$W^{[2]}$的维度为 4 x 3，$b^{[2]}$ 的维度为 4 x 1 …..

  由此，可以归纳出一个维度公式，即对于第k层中(k>0），有

  $$\begin{array}\\ W^{[k]}的维度 = n^{[k]} * n^{[k-1]} \\ b^{[k]}的维度 = n^{[k]} * 1 \end{array}$$

  得到每个参数的维度后，就可以很方便的检验运算是否正确咯。

超参数

• 什么是超参数

  • 在整个NN中，有许多参数，比如$W^{[1]},b^{[1]},W^{[2]},b^{[2]}$等等，还有一些其他参数，比如$学习率\alpha，迭代次数\#iterations,隐藏层数L，隐藏单元个数n^{[l]},激活函数等等$。 而这些这参数都会影响到最终的W,b的结果，所以这些参数就被称作超参数。实际上还有很多超参数，具体的会在之后详细谈及。

• 超参数的作用

  • 在深度学习算法中的超参数如何取值是一个以实验为依据的过程，有时候，可能依赖直觉，比如设置$\alpha = 0.01$,然后实际操作了一下，得到了某个结果，但是对这个结果不满意，于是把$\alpha$的值增加到0.05。

    大部分情况下，都很难提前知道这些超参数的最优解，所以具体的取值其实是一个基于试验的过程，在过程中发现新的最优解。

多层NN反向传播

• 在这里，我们具体讨论一下，关于多层网络的反向传播算法。对于前向传播，相信大家应该都很熟悉了，这列就不过多陈述了。主要还是反向传播（Back Propagation，简称BP）。在BP中，第一层的输入应该是在$da^{[l]}$,而输出是$dW^{[l]},db^{[l]}$。

  假设一共有L层网络，Y为真实的label，则在第L层，有

  $$\begin{array} \\ dZ^{[L]} = A^{[L]} - Y \\ dW^{[L]} = \left(\frac{1}{m}\right) dZ^{[L]} A^{[L-1]T} \\ db^{[L]} = \left(\frac{1}{m}\right)dZ^{[L]} \end{array}$$

对于接下来的L-1层，有

$$\begin{array} \\ dZ^{[L-1]} = W^{[L]T} dZ^{[L]} * g^{[L]'}(Z^{[L-1]}) \\ dW^{[l-1]} = \left(\frac{1}{m}\right) dZ^{[L-1]} * A^{[L-2]T} \\ db^{[L-1]} = \left(\frac{1}{m}\right)dZ^{[L-1]} \end{array}$$

这里公式是针对所有样本而言，且认为是做二元分类，即最后的激活函数为sigmoid。 * 代表 对应元素相乘，即A矩阵为 m x n, B矩阵为 m x n ，那么A * B 依旧是 m x n的矩阵。有了对应的梯度，我们就可以利用for循环来实现对L层网络的反向传播，这里要注意第一次梯度下降时要分开。